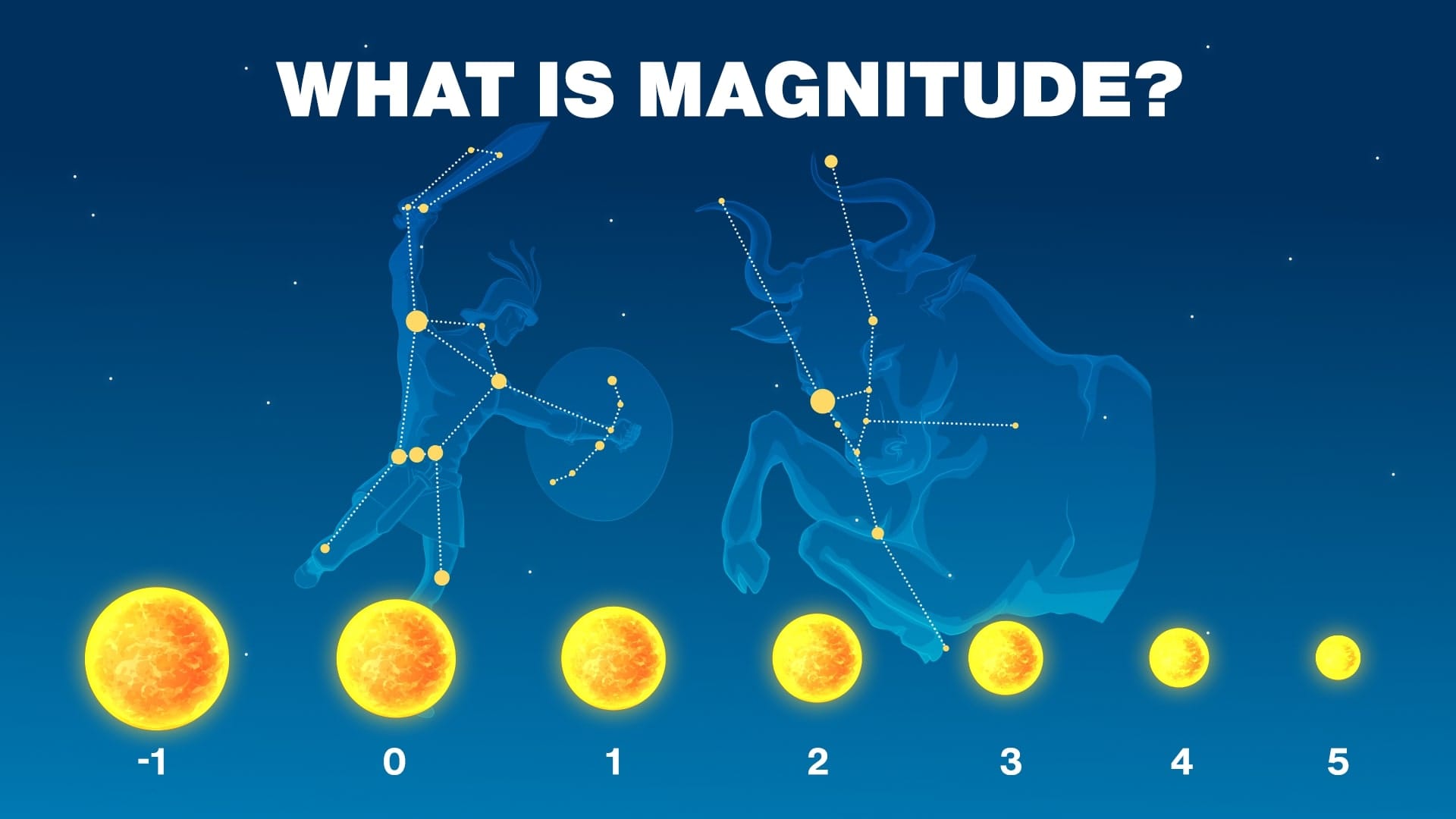
How is Brightness in Astronomy Measured
By knowing a celestial object’s brightness, you can tell if this object is visible or not. But how do you actually measure this brightness? Which measurement is used in what case? Let’s sort it all out so you can observe the night sky like a pro! P.S. To quickly find out the brightness of any object in the sky, get the Sky Tonight app.
Contents
- What is magnitude
- How is magnitude measured
- Surface brightness
- Limiting apparent magnitudes: guide for observers
- Bottom line
What is magnitude
In astronomy, stellar magnitude is a measure of how bright or dim an object appears in the sky.
Notice that we used the term “appears” in the definition. It is because magnitude, as we usually mean it, does not tell how bright that object really is. It refers to how bright it seems to be.
You should never confuse magnitude with luminosity (L) — the brightness of an object in space.
Absolute vs. Apparent magnitude
Astronomers divide magnitude into two general types: apparent and absolute.
- Apparent magnitude (m, often simply “magnitude” or mag) is the brightness of a celestial object as seen from Earth.
- Absolute magnitude (M) is how bright an object would be if it was a set distance of 10 parsecs¹ from Earth. Seems that astronomers chose a distance of 10 parsecs because that was close to the average distance of stars whose distances were known in 1902. Absolute magnitude for planets and small Solar System bodies (H) is frequently quoted based on a distance of 1 AU from the observer.
¹A unit of distance in astronomy, 1 parsec equals 3.26 light-years or 3.09 × 10¹³ km (1.92 × 10¹³ miles).
It’s important to point out that an object’s absolute magnitude is measured without extinction (or dimming) of its light due to absorption by interstellar matter and cosmic dust.
So the apparent magnitude depends on an object’s intrinsic luminosity, its distance, and the extinction reducing its brightness. The absolute magnitude allows us to compare the intrinsic luminosity of objects (in a given range of the spectrum) by hypothetically placing all objects at a standard reference distance from the observer.
Let’s take our Sun and Rigel. The Sun appears way brighter than Rigel in our sky so its apparent magnitude is higher (magnitude −26.8 and 0.18, respectively). However, if we placed both the Sun and Rigel at 10 parsecs away from the Earth, Rigel would impressively outshine the Sun. That’s because the distant star has a higher absolute magnitude: -6.69 vs 4.83 for the Sun.
Here are some more examples:
- Alpha Centauri: m = −0.3 vs M = 4.1
- Canopus: m = −0.7 vs M = −3.1
- Deneb: m = 1.26 vs M = −7.1
- Neptune: m = 7.8 (avg) vs H = −6.9
Apparent magnitude values are expressed as a number without a unit; when you see something like "Antares has a magnitude of 1.09", it means that the apparent magnitude is implied. This can be written more concisely as "Antares (mag 1.09)", "Antares (1.09 m)" or "Antares (m = 1.09)". When referring to magnitude types other than apparent, astronomers specify the type by writing the magnitude type with a phrase or abbreviation letter: "Antares has an absolute magnitude of −5.28" or "Antares (M = −5.28)". They also use the letters in formulas.
By the way, apparent magnitude can be measured both with the naked eye and with a telescope; both in the visual range of the spectrum and in other ranges (photographic, UV, IR). In this case, "apparent" means "observable" and does not refer specifically to the human eye. If we’re only considering what the human eye can see, then we’re measuring visual magnitude. However, many popular science sources use these terms interchangeably.
How is magnitude measured
Magnitude scale
In 137 CE, the ancient astronomer Ptolemy classified stars on a six-point scale from one (brightest) to six (faintest, barely visible to the naked eye) and coined the term magnitude. Initially, this system grouped stars into six distinct groups without distinguishing brightness within a group. Today, we use a refined version of this magnitude scale.
Ptolemy’s scale is a system of how relatively bright celestial objects appear to be. Such a system requires a zero point or a reference star. Traditionally, Vega, with an apparent magnitude of 0.0, was taken as this reference star.
Of course, with the development of telescopes, astronomers expanded this scale to include much dimmer celestial bodies, such as faint nebulae and distant galaxies.
Astronomers also extended the scale to cover brighter objects in the sky, like the Sun, the Moon, and some planets. Since Vega was considered the zero-magnitude star, astronomers assigned negative values to objects brighter than Vega. Here are some examples of apparent magnitude values for bright objects:
- Sun: –26.5
- Full Moon: –12.5 (avg)
- Venus: –4.3 (avg)
- Jupiter: –2.7 (avg)
- Sirius: –1.44
- Vega: 0.0
- Deneb: 1.25
So this magnitude scale might be confusing, just remember that the larger the number, the dimmer the object. The brightest objects have negative magnitudes.
How stars are distributed by magnitude
You might have noticed that there are far more dimmer stars than there are brighter ones in our night sky. Here’s a simplified breakdown of star numbers by their stellar magnitudes:
- Magnitude from –1.5 to –0.5: 2 stars
- Magnitude from –0.5 to 0.5: 6 stars
- Magnitude from 0.5 to 1.5: 14 stars
- Magnitude from 1.5 to 2.5: 71 stars
- Magnitude from 2.5 to 3.5: 190 stars
- Magnitude from 3.5 to 4.5: 610 stars
- Magnitude from 4.5 to 5.5: 1,929 stars
- Magnitude from 5.5 to 6.5: 5,946 stars
Note that these numbers represent all the stars visible to the naked eye in the entire sky. Since we can only see half the sky at any moment, the actual number of stars you can see at one time is different.
How apparent magnitude scale is calculated
We know that a magnitude 1 star is brighter than a magnitude 2 star. But how much brighter?
The magnitude scale is logarithmic, where a difference of 5 magnitudes always corresponds to a brightness change by a factor of 100. This means that a star of magnitude 1 is 100 times brighter than a magnitude 6 star, and similarly, a star of magnitude 2 is 100 times brighter than a magnitude 7 star.
Here’s how the scale works:
- A one-magnitude difference (like from 1 to 2) changes the brightness by approximately 2.5 times.
- This factor compounds with each step, meaning a magnitude 3 star is 6.25 times fainter than a magnitude 1 star (2.5 x 2.5=6.25).
But if you use a calculator, you'll see that the numbers don't quite add up. That's because 2.5 is a simplification; the precise number is 100^(1/5) ≈ 2.51188643150958. In most sources, you'll see this number shortened to 2.5 or 2.512. Here is the change in magnitude between stars with differences of 1, 2, 3, 4, and 5 magnitudes:
- 1 magnitude difference: 2.512 ≈ 2.5
- 2 magnitudes difference: 2.512 x 2.512 ≈ 6.3
- 3 magnitudes difference: 2.512 x 2.512 x 2.512 ≈ 15.8
- 4 magnitudes difference: 2.512 x 2.512 x 2.512 x 2.512 ≈ 39.8
- 5 magnitudes difference: 2.512 x 2.512 x 2.512 x 2.512 x 2.512 ≈ 100
Now, we can calculate how bright the Full Moon is compared to Venus, the next brightest object in the night sky. Their magnitudes vary slightly, so let’s take magnitudes –12.7 for the Full Moon and –4.6 for Venus.
The difference in magnitudes of the Full Moon and Venus is –4.6 – (–12.7) = 8.1 units.
A difference in magnitude 1 increases the brightness by about 2.512 times, so an increase in magnitude by 8.1 times will increase the brightness by (2.512)^8.1 times, which is ≈1,700.
So, the Full Moon is about 1,700 times brighter than Venus! If we use the general equation for comparing brightness based on stellar magnitudes, it can be expressed as:
Iᴬ / Iᴮ ≈ 2.512^(mᴮ – mᴬ)
Here Iᴬ and Iᴮ represent the intensities (or brightness) of objects A and B, respectively, and mᴮ, mᴬ are their magnitudes.
How to find the apparent magnitude
To define an object’s precise apparent magnitude, astronomers measure this object’s flux or intensity (the total amount of energy per unit area arriving at the telescope’s detector per second). Then, they compare how relatively bright the source appears to be by comparing it with the reference star, using the following formula:
m₁ – m₀ = –2.5 × log₁₀ (F₁ / F₀)
where m is the magnitude (as we already know) and F is flux. I is used instead of F in many sources, as astronomers use the term "flux" for what is often called "intensity" in physics.
As we already mentioned, the reference star (the zero point) was chosen to be the star Vega (i.e., F₀ is the flux of Vega, and m₀ is the magnitude of Vega).
With the advent of accurate photometers and cameras, astronomers realized that even Vega wasn’t a perfect reference star. Its brightness varied over time by ~0.03 magnitudes. So, for the sake of accuracy, astronomers came up with the zero point based on a theoretical source with constant flux. However, for visual observations, Vega can still serve as a standard of zero magnitude.
There is a whole branch of science dedicated to the measurement of the brightness of stars and other celestial objects — photometry.
Different magnitude systems: spectral ranges
Magnitude depends on the receiver's spectral sensitivity (eye, photoelectric detector, photographic plate, etc.).
There are many systems of magnitudes with respect to spectral ranges, each differing in the choice of a particular measurement range.
Visual magnitude (mᵥ) describes how a star looks to the eye.
Photographic magnitude (mₚ) is measured from an image of a star on a photographic plate obtained without additional light filters. Since the photo emulsion is sensitive to blue rays and insensitive to red rays, blue stars appear brighter (than they seem to the eye) on the photographic plate.
By comparing the brightnesses of a source measured in different bands of the spectrum, astronomers can learn its color, estimate its surface temperature (if it is a star) or albedo (if it is a planet), determine the degree of interstellar light absorption, and other important characteristics.
Therefore, standard photometric range systems, mainly determined by the selection of light filters, have been developed. The most popular is the three-color UBV system: ultraviolet (U), blue (B), and visual (V). The visual range is very close to the photovisual range, and the blue range is close to the photographic range.
In addition to spectrally sensitive receivers, there are bolometers that measure bolometric magnitude — the radiation flux summed over all ranges of the spectrum. The bolometric magnitude allows to calculate the luminosity of an object if the distance to the source and the degree of interstellar absorption are known.
Surface brightness
Until now, we have mainly discussed pinpoint sources of light, such as stars and planets. But not all objects in the night sky are as compact as stars.
Some celestial objects extend over a wide area, like galaxies and nebulae. Taking all of the light flux of an object and determining a magnitude from it can be misleading.
Therefore, in this case, apparent magnitude doesn’t really help answer the main question: how bright is this object for the observer on the Earth?
For example, the Andromeda Galaxy has an apparent magnitude of 3.4, which should be visible to the naked eye even in a light-polluted area! However, this doesn’t match what we see in the night sky.
Astronomers tackle this problem using surface brightness, a measure of brightness per unit area. This averages out the brightness of the object across the entire object.
Surface brightness (SB) quantifies the apparent brightness or flux density per unit angular area of a spatially extended object such as a galaxy or nebula or of the night sky background.
An object's surface brightness is often expressed either in magnitudes per square arcsecond (mag/arcsec²) or magnitudes per square arcminute (mag/arcmin²). Here are some objects with the apparent magnitude and lowest (brightest) surface brightness:
- Orion Nebula: 4 m vs 17 mag/arcsec²
- Andromeda Galaxy: 3.4 m vs 11 mag/arcsec²
- Triangulum Galaxy: 5.7 m vs 14.2 mag/arcsec²
- Bode’s Galaxy: 6.9 m vs 25 mag/arcsec²
However, the surface brightness of an object is rarely mentioned, even though it’s important for visual observations.
Interesting fact: eyes are better at detecting light from a diffuse, or spread out, source (like galaxies) than from a point source (like a star).
This means that it is easier to see objects with a diffuse brightness than objects with a point source. The core of the Andromeda Galaxy is ~11 mag/arcsec² but is still visible to the eye. The outer edge of the galaxy can be seen with telescopes at 22 mag/arcsec², a much dimmer target!
Limiting apparent magnitudes: guide for observers
The limiting magnitude is the apparent magnitude of the faintest object visible in the sky. Here is a cheat sheet that is useful for any amateur astronomer. It will help you with your observations.
- Naked-eye limit for comets: 4
- Naked-eye limit for planets and stars: 6.5
- 7×50 binocular limit: 10
- 35mm aperture telescope limit: 11.3
- 60mm aperture telescope limit: 12.3
- 102mm aperture telescope limit: 13.3
Note that light pollution has a huge effect on the range of stellar magnitudes you can see! We have provided numbers for observing conditions close to ideal, but they may be different for your location. Learn how to indicate how dark or bright your sky is with our handy scale.
By the way, to find out your telescope's limiting magnitude (the faintest magnitude you can see with it under perfect conditions), you can use the Telescope Limiting Magnitude Calculator.
Bottom line
Stellar magnitude is one of the most important concepts in observational astronomy because it answers one of the most important questions: "How bright is this object?". To classify objects by brightness, astronomers use the logarithmic magnitude scale, where the brightest objects have the lowest values. By understanding magnitudes, amateur observers can improve their ability to identify and compare the brightness of celestial objects.
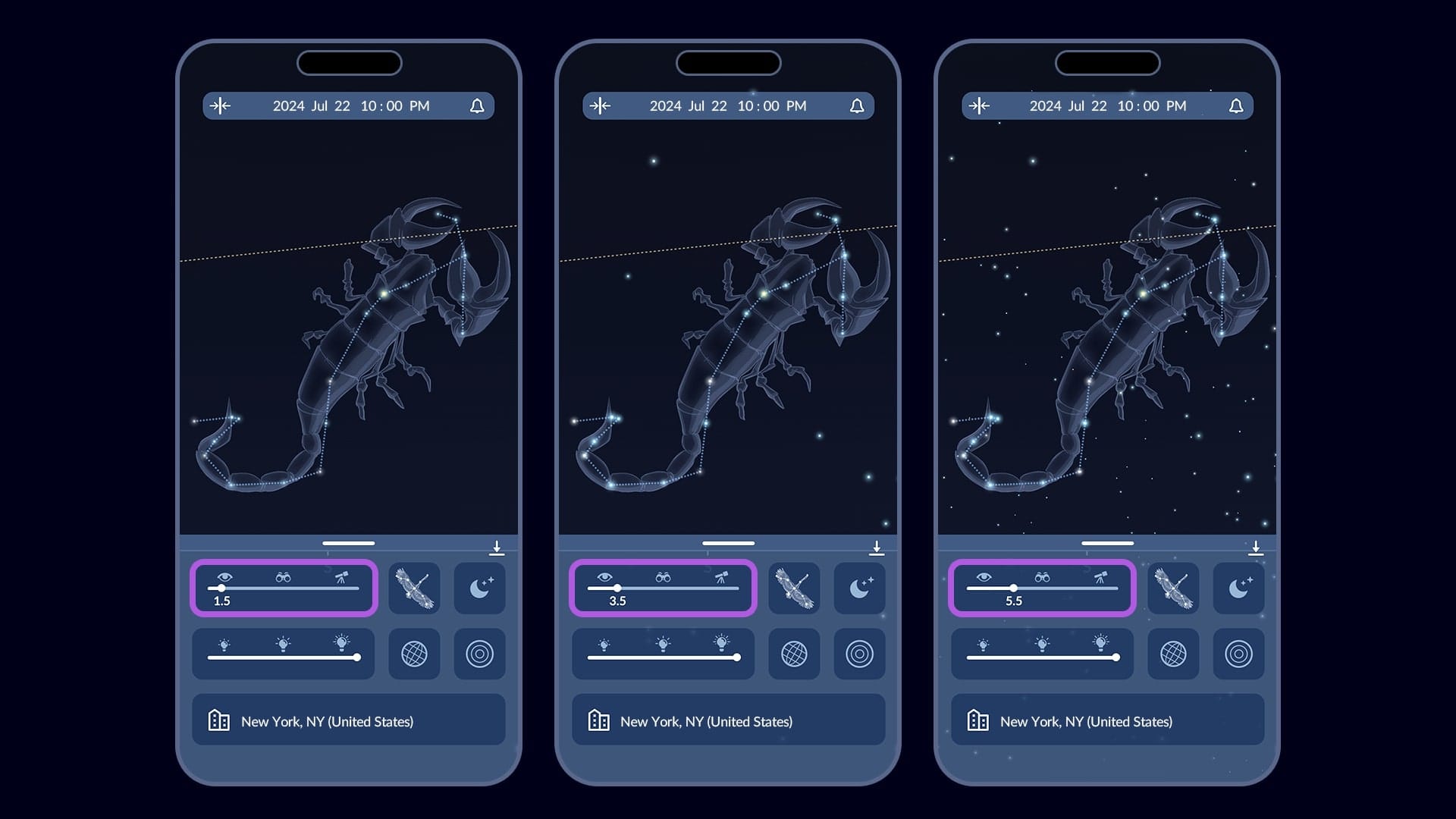
To see the faintest objects in the sky right now, get the free Sky Tonight app — it allows you to change the magnitude limit of what is displayed on your screen using a slider at the bottom. The app's slider features icons (eye, binoculars, telescope) so you can filter out objects by their visibility.
