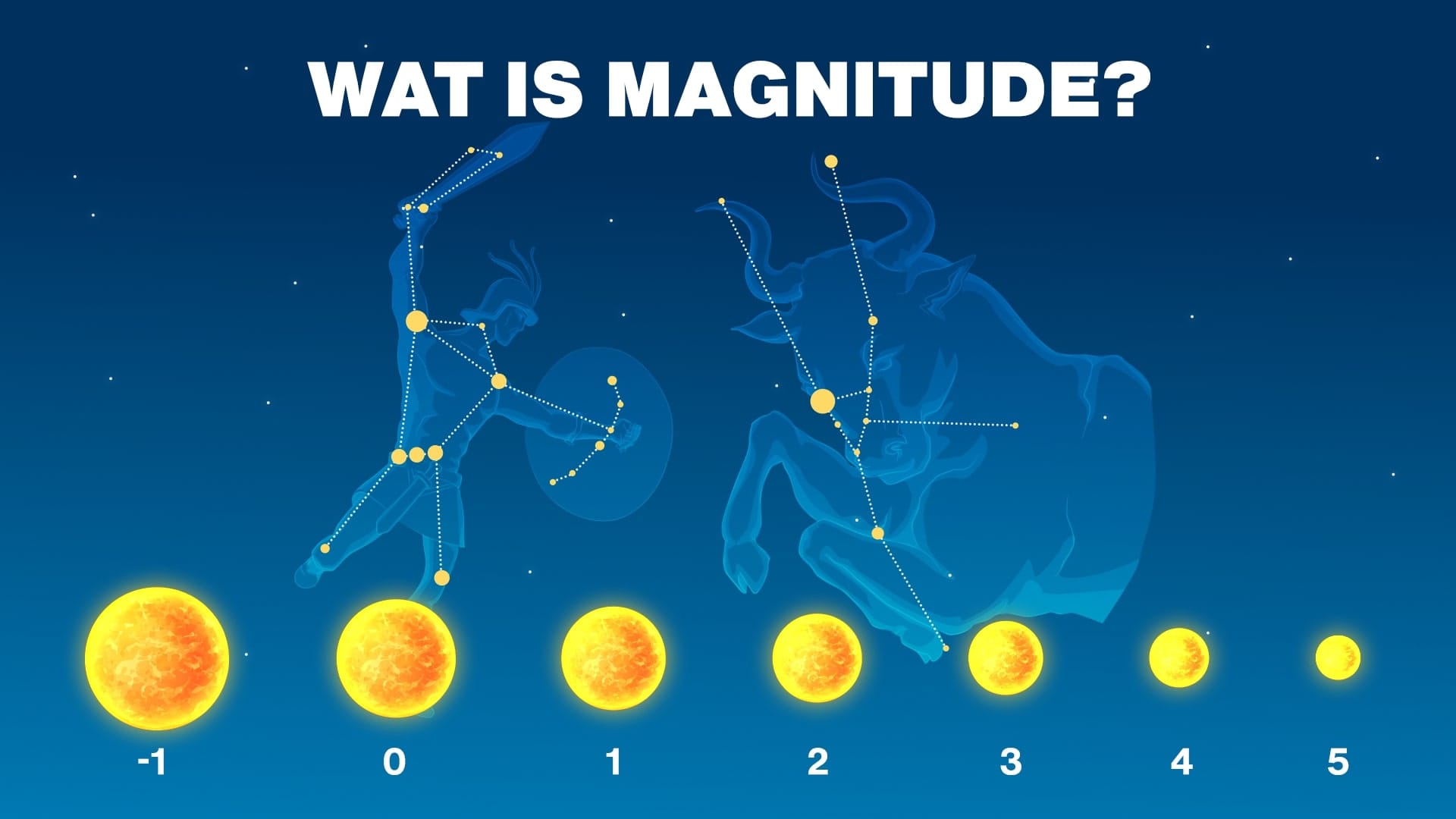
Magnitude in de astronomie: hoe wordt helderheid gemeten
Door de helderheid van een hemellichaam te kennen, kun je bepalen of dit object zichtbaar is of niet. Maar hoe meet je deze helderheid eigenlijk? Welke meting wordt in welk geval gebruikt? Laten we alles op een rijtje zetten, zodat je als een professional de nachtelijke hemel kunt observeren! P.S. Om snel de helderheid van een willekeurig object aan de hemel te vinden, download de Sky Tonight app.
Inhoud
- Wat is magnitude?
- Hoe magnitude wordt gemeten
- Oppervlaktehelderheid
- Beperkende schijnbare magnitudes: gids voor waarnemers
- Conclusie
Wat is magnitude?
In de astronomie is magnitude een maat voor hoe helder of dof een object aan de hemel verschijnt.
Merk op dat we in de definitie het woord “lijkt” gebruiken. Dat komt omdat magnitude, zoals we het meestal bedoelen, niet aangeeft hoe helder een object werkelijk is, maar hoe helder het lijkt voor een waarnemer.
Verwar magnitude nooit met luminositeit (L) — de totale hoeveelheid lichtenergie die een object elke seconde in alle richtingen uitstraalt.
Opmerking: Wanneer astronomen het over de helderheid van een object hebben, geven ze meestal aan welk deel van het lichtspectrum ze meten. Licht kan worden verdeeld in verschillende gebieden op basis van golflengte — bijvoorbeeld ultraviolet (kort), blauw of zichtbaar (wat het menselijk oog kan zien). Om consistente metingen te garanderen, gebruiken astronomen standaardfilters die deze golflengten isoleren, bekend als de U-, B- en V-banden (ultraviolet, blauw en visueel). De V-band komt ongeveer overeen met de gevoeligheid van het menselijk oog en is de meest gebruikte.
Tenzij anders vermeld, verwijzen alle magnitudewaarden in dit artikel naar de V-band (visueel).
Absolute vs. schijnbare magnitude
Astronomen verdelen magnitude in twee hoofdtypen: schijnbaar en absoluut.
- Schijnbare magnitude (m, vaak gewoon “magnitude” of mag) is de helderheid van een hemelobject zoals gezien vanaf de aarde.
- Absolute magnitude (M) is hoe helder een object zou zijn als het zich op een vaste afstand van 10 parsec¹ van de aarde bevond. Astronomen kozen 10 parsec omdat dit rond 1902 ongeveer de gemiddelde afstand was van sterren waarvan de afstand bekend was. Voor planeten en kleine objecten in het zonnestelsel gebruiken astronomen het symbool H, dat aangeeft hoe helder het object zou lijken als het zich op één astronomische eenheid (AE) van zowel de zon als de waarnemer bevond en volledig verlicht was — dus als zon, object en waarnemer perfect op één lijn stonden.
¹Een eenheid van afstand in de astronomie, 1 parsec is gelijk aan 3,26 lichtjaren of 3,09 × 10¹³ km.
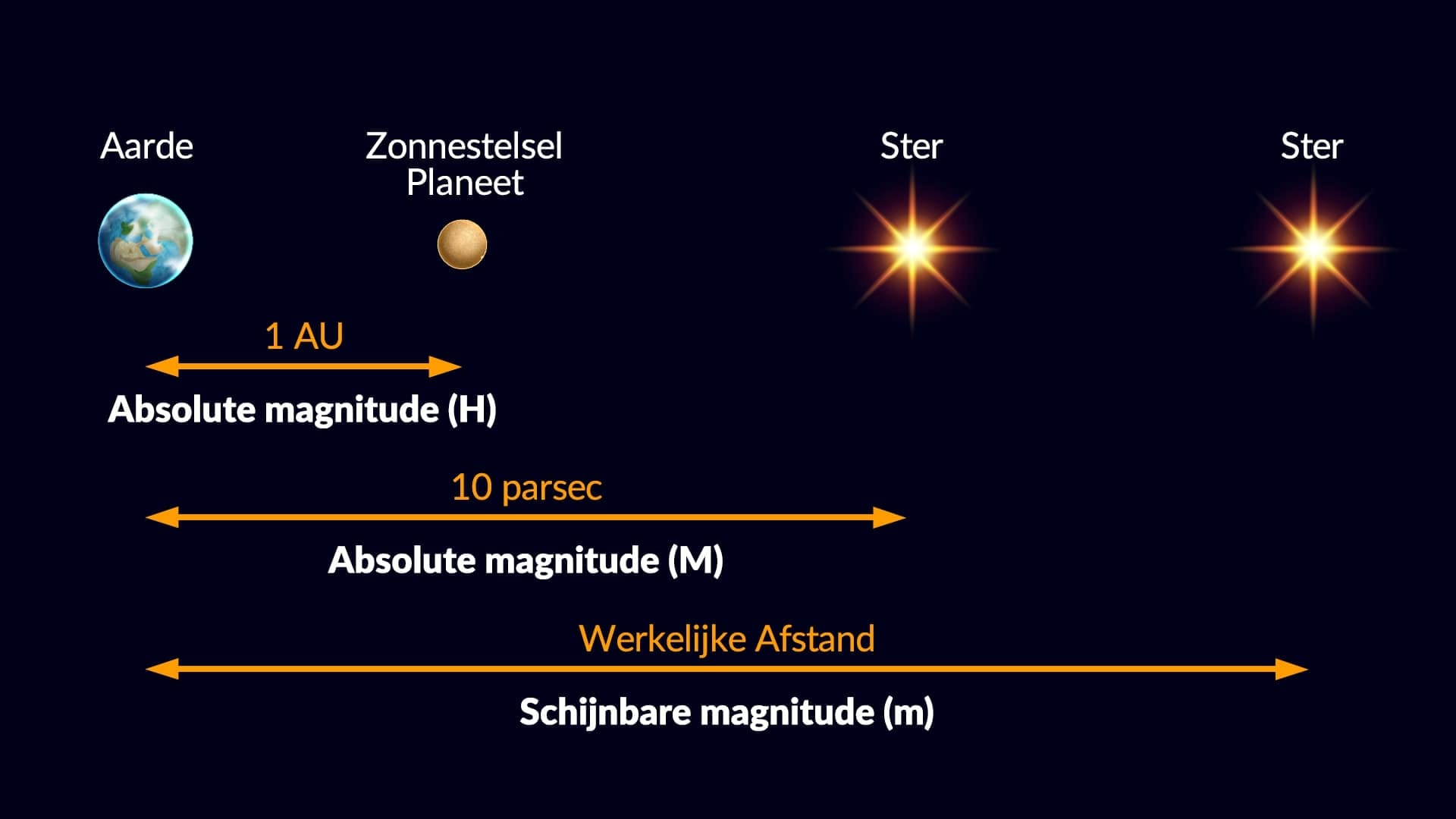
Het is belangrijk om te benadrukken dat de absolute magnitude van een object wordt gemeten zonder extinctie (of verduistering) van zijn licht door absorptie door interstellair materiaal en kosmisch stof.
Dus de schijnbare magnitude hangt af van de intrinsieke luminositeit van een object, zijn afstand en de extinctie die zijn helderheid vermindert. De absolute magnitude stelt ons in staat de intrinsieke luminositeit van objecten (binnen een bepaald bereik van het spectrum) te vergelijken door hypothetisch alle objecten op een standaard referentieafstand van de waarnemer te plaatsen.
Laten we onze Zon en Rigel nemen. De Zon lijkt veel helderder dan Rigel in onze hemel, dus zijn schijnbare magnitude is hoger (magnitude −26.8 en 0.18, respectievelijk). Echter, als we zowel de Zon als Rigel op 10 parsecs afstand van de Aarde zouden plaatsen, zou Rigel indrukwekkend helderder schijnen dan de Zon. Dat komt omdat de verre ster een hogere absolute magnitude heeft: -6.69 versus 4.83 voor de Zon.
Hier zijn nog wat voorbeelden:
- Alpha Centauri: m = −0.3 vs M = 4.1
- Canopus: m = −0.7 vs M = −3.1
- Deneb: m = 1.26 vs M = −7.1
- Neptunus: m = 7.8 (gem) vs H = −6.9
Schijnbare magnitude-waarden worden uitgedrukt als een getal zonder eenheid; als je zoiets ziet als "Antares heeft een magnitude van 1.09", betekent dit dat de schijnbare magnitude wordt verondersteld. Dit kan bondiger worden geschreven als "Antares (mag 1.09)", "Antares (1.09 m)" of "Antares (m = 1.09)". Bij het verwijzen naar andere magnitude-types dan schijnbaar, specificeren astronomen het type door de magnitudetype te schrijven met een zin of afkorting: "Antares heeft een absolute magnitude van −5.28" of "Antares (M = −5.28)". Ze gebruiken ook de letters in formules.
De schijnbare magnitude kan overigens zowel met het blote oog als met instrumenten worden gemeten en kan betrekking hebben op elk deel van het spectrum (visueel, fotografisch, ultraviolet, infrarood, enz.). In deze context betekent “schijnbaar” dus “zoals gezien vanaf de positie van de waarnemer, ongeacht het gebruikte instrument”. Wanneer we specifiek verwijzen naar helderheid zoals die door het menselijk oog wordt waargenomen, gebruiken we de term “visuele magnitude”. Veel populaire bronnen gebruiken deze termen echter door elkaar, ook al zijn ze niet helemaal hetzelfde.
Hoe magnitude wordt gemeten
Magnitudeschaal
De magnitudeschaal kent een lange geschiedenis. Oude astronomen zoals Hipparchus (2e eeuw v.Chr.) en Ptolemaeus (2e eeuw n.Chr.) gebruikten al een schaal met zes niveaus: van één (de helderste) tot zes (de zwakste, net zichtbaar met het blote oog).
Aanvankelijk deelde dit systeem sterren in zes groepen in, zonder rekening te houden met helderheidsverschillen binnen elke groep. Tegenwoordig gebruiken we een veel verfijndere versie van die schaal.
Die oude schaal was bedoeld om te bepalen hoe helder hemelobjecten ten opzichte van elkaar lijken. Een dergelijk systeem heeft een nulpunt of referentiester nodig. Traditioneel werd Vega, met een schijnbare magnitude van 0,0, als referentie gebruikt.
Met de komst van telescopen breidden astronomen de schaal uit om veel zwakkere objecten, zoals nevels en verre sterrenstelsels, te kunnen opnemen.
Ze pasten de schaal ook aan voor veel helderdere objecten, zoals de zon, de maan en enkele planeten. Omdat Vega de ster met magnitude nul was, kregen objecten die helderder zijn dan Vega negatieve waarden. Hier enkele voorbeelden van schijnbare magnitudes:
- Zon: –26,7
- Volle maan: –12,7 (gemiddeld)
- Venus: tot –4,8 (afhankelijk van de fase)
- Jupiter: –2,9 (in oppositie)
- Sirius: –1,4
- Vega: 0,0
- Deneb: 1,2
Dus deze magnitudeschaal kan verwarrend zijn, onthoud gewoon dat hoe groter het getal, hoe zwakker het object. De helderste objecten hebben negatieve magnitudes.

Hoe sterren worden verdeeld door magnitude?
Je hebt misschien opgemerkt dat er veel meer zwakkere sterren zijn dan er heldere zijn in onze nachtelijke hemel. Hier is een vereenvoudigde uitsplitsing van het aantal sterren per hun magnitudes:
- Magnitude van –1.5 tot –0.5: 2 sterren
- Magnitude van –0.5 tot 0.5: 6 sterren
- Magnitude van 0.5 tot 1.5: 14 sterren
- Magnitude van 1.5 tot 2.5: 71 sterren
- Magnitude van 2.5 tot 3.5: 190 sterren
- Magnitude van 3.5 tot 4.5: 610 sterren
- Magnitude van 4.5 tot 5.5: 1,929 sterren
- Magnitude van 5.5 tot 6.5: 5,946 sterren
Let op dat deze aantallen alle sterren vertegenwoordigen die met het blote oog zichtbaar zijn in de hele hemel. Aangezien we slechts de helft van de hemel op elk moment kunnen zien, is het daadwerkelijke aantal sterren dat je op een bepaald moment kunt zien anders.
Hoe wordt de schijnbare magnitudeschaal berekend?
We weten dat een ster van magnitude 1 helderder is dan een ster van magnitude 2. Maar hoeveel helderder?
De magnitudeschaal is logaritmisch, waarbij een verschil van 5 magnitudes altijd overeenkomt met een helderheidsverandering met een factor 100. Dit betekent dat een ster van magnitude 1 100 keer helderder is dan een ster van magnitude 6, en evenzo, een ster van magnitude 2 is 100 keer helderder dan een ster van magnitude 7.
Hier is hoe de schaal werkt:
- Een verschil van één magnitude (zoals van 1 naar 2) verandert de helderheid met ongeveer 2.5 keer.
- Deze factor vermenigvuldigt zich met elke stap, wat betekent dat een ster van magnitude 3 6.25 keer zwakker is dan een ster van magnitude 1 (2.5 x 2.5=6.25).
Als we deze schaal uitbreiden tot vijf magnitudes, wordt de factor 2.5, verheven tot de vijfde macht, wat ongeveer 100 is. Maar als je een rekenmachine gebruikt, zul je zien dat de getallen niet helemaal kloppen. Dat komt omdat 2.5 een vereenvoudiging is; het precieze getal is 100^(1/5) ≈ 2.51188643150958. In de meeste bronnen zie je dit getal afgerond op 2.5 of 2.512. Hier is de verandering in magnitude tussen sterren met verschillen van 1, 2, 3, 4, en 5 magnitudes:
- 1 magnitude verschil: 2.512 ≈ 2.5
- 2 magnitudes verschil: 2.512 x 2.512 ≈ 6.3
- 3 magnitudes verschil: 2.512 x 2.512 x 2.512 ≈ 15.8
- 4 magnitudes verschil: 2.512 x 2.512 x 2.512 x 2.512 ≈ 39.8
- 5 magnitudes verschil: 2.512 x 2.512 x 2.512 x 2.512 x 2.512 ≈ 100
Nu kunnen we berekenen hoe helder de Volle Maan is vergeleken met Venus, het volgende helderste object aan de nachthemel. Hun magnitudes variëren enigszins, dus laten we magnitudes –12.7 voor de Volle Maan en –4.6 voor Venus nemen.
Het verschil in magnitudes van de Volle Maan en Venus is –4.6 – (–12.7) = 8.1 eenheden.
Een verschil in magnitude 1 verhoogt de helderheid met ongeveer 2.512 keer, dus een toename in magnitude met 8.1 keer zal de helderheid verhogen met (2.512)^8.1 keer, wat ≈1,700 is.
Dus, de Volle Maan is ongeveer 1,700 keer helderder dan Venus! Als we de algemene vergelijking gebruiken om helderheid te vergelijken op basis van magnitudes, kan dit worden uitgedrukt als:
Iᴬ / Iᴮ ≈ 2.512^(mᴮ – mᴬ)
Hier Iᴬ en Iᴮ vertegenwoordigen de intensiteiten (of helderheid) van objecten A en B, respectievelijk, en mᴮ, mᴬ zijn hun magnitudes.
Hoe vind je de schijnbare magnitude?
Om de precieze schijnbare magnitude van een object te vinden, meten astronomen de flux of intensiteit (de totale hoeveelheid energie per oppervlakte-eenheid die per seconde op de detector van de telescoop aankomt). Vervolgens vergelijken ze hoe relatief helder de bron lijkt te zijn door deze te vergelijken met de referentiester, met behulp van de volgende formule:
m₁ – m₀ = –2.5 × log₁₀ (F₁ / F₀)
waarbij m de magnitude is (zoals we al weten) en F de flux is. I wordt vaak gebruikt in plaats van F in veel bronnen, aangezien astronomen de term "flux" gebruiken voor wat vaak "intensiteit" wordt genoemd in de natuurkunde.
Zoals we al vermeldden, werd de referentiester (het nulpunt) gekozen als de ster Vega (d.w.z., F₀ is de flux van Vega, en m₀ is de magnitude van Vega).
Met de komst van nauwkeurige fotometers en camera’s ontdekten astronomen dat zelfs Vega geen perfecte referentie was, omdat haar helderheid licht varieert (ongeveer 0,03 magnitudes). Om consistentie tussen verschillende golflengtebanden te garanderen, werd het nulpunt later gedefinieerd op basis van een theoretische constante lichtbron in plaats van een echte ster. Voor visuele waarnemingen kan Vega echter nog steeds worden beschouwd als de standaardster met magnitude nul.
Er is een hele tak van wetenschap gewijd aan het meten van de helderheid van sterren en andere hemellichamen — fotometrie.
Verschillende magnitudesystemen: spectraal bereiken
Magnitude hangt af van de spectrale gevoeligheid van de ontvanger (oog, foto-elektrische detector, fotografische plaat, enz.).
Er zijn veel systemen van magnitudes met betrekking tot spectraal bereiken, elk verschillend in de keuze van een bepaald meetbereik.
Visuele magnitude (mᵥ) beschrijft hoe een ster eruitziet voor het oog.
Fotografische magnitude (mₚ) wordt gemeten van een afbeelding van een ster op een fotografische plaat, verkregen zonder extra lichtfilters. Aangezien de foto-emulsie gevoelig is voor blauwe stralen en ongevoelig voor rode stralen, verschijnen blauwe sterren helderder (dan ze lijken voor het oog) op de fotografische plaat.
Door de helderheden van een bron te vergelijken die gemeten zijn in verschillende banden van het spectrum, kunnen astronomen de kleur ervan leren, de oppervlaktetemperatuur schatten (als het een ster is) of albedo (als het een planeet is), de mate van interstellaire lichtabsorptie bepalen, en andere belangrijke kenmerken.
Daarom zijn standaard fotometrische bereiksystemen, voornamelijk bepaald door de selectie van lichtfilters, ontwikkeld. Het meest populaire is het driekleuren UBV-systeem: ultraviolet (U), blauw (B) en visueel (V). Het visuele bereik komt zeer dicht bij het fotovisuele bereik, en het blauwe bereik ligt dicht bij het fotografische bereik.
Naast spectraalgevoelige ontvangers zijn er bolometers die de bolometrische magnitude meten — de stralingsflux opgeteld over alle bereiken van het spectrum. De bolometrische magnitude maakt het mogelijk om de luminositeit van een object te berekenen als de afstand tot de bron en de mate van interstellaire absorptie bekend zijn.
Oppervlaktehelderheid
Tot nu toe hebben we voornamelijk gesproken over puntbronnen van licht, zoals sterren en planeten. Maar niet alle objecten aan de nachtelijke hemel zijn zo compact als sterren.
Sommige hemellichamen strekken zich uit over een groot gebied, zoals sterrenstelsels en nevels. Alle lichtflux van een object nemen en daaruit een magnitude bepalen kan misleidend zijn.
Daarom helpt schijnbare magnitude in dit geval niet echt om de hoofdvraag te beantwoorden: hoe helder is dit object voor de waarnemer op Aarde?
Bijvoorbeeld, het Andromeda-sterrenstelsel heeft een schijnbare magnitude van 3.4, wat zichtbaar zou moeten zijn met het blote oog, zelfs in een lichtvervuilde omgeving! Dit komt echter niet overeen met wat we in de nachtelijke hemel zien.

Astronomen pakken dit probleem aan met behulp van oppervlaktehelderheid, een maat voor helderheid per oppervlakte-eenheid. Dit middelt de helderheid van het object over het hele object.
Oppervlaktehelderheid (SB) kwantificeert de schijnbare helderheid of fluxdichtheid per eenheid hoekoppervlakte van een ruimtelijk uitgestrekt object zoals een sterrenstelsel of nevel of van de achtergrond van de nachtelijke hemel.
De oppervlaktehelderheid van een object wordt vaak uitgedrukt in magnitudes per vierkante boogseconde (mag/arcsec²) of magnitudes per vierkante boogminuut (mag/arcmin²). Hier zijn enkele objecten met de schijnbare magnitude en laagste (helderste) oppervlaktehelderheid:
- Orionnevel: 4 m vs 17 mag/arcsec²
- Andromedasterrenstelsel: 3.4 m vs 11 mag/arcsec²
- Driehoekig Sterrenstelsel: 5.7 m vs 14.2 mag/arcsec²
- Bode’s Sterrenstelsel: 6.9 m vs 25 mag/arcsec²
Echter, de oppervlaktehelderheid van een object wordt zelden vermeld, ook al is het belangrijk voor visuele waarnemingen.

Interessant feit: ogen zijn beter in staat om licht van een diffuse, of uitgespreide, bron (zoals sterrenstelsels) te detecteren dan van een puntbron (zoals een ster).
Dit betekent dat het gemakkelijker is om objecten met een diffuse helderheid te zien dan objecten met een puntbron. De kern van het Andromeda-sterrenstelsel is ~11 mag/arcsec² maar is nog steeds zichtbaar voor het oog. De buitenrand van het sterrenstelsel kan met telescopen worden gezien bij 22 mag/arcsec², een veel zwakker doel!
Beperkende schijnbare magnitudes: gids voor waarnemers
De beperkende magnitude is de schijnbare magnitude van het zwakste object dat aan de hemel zichtbaar is. Hier is een spiekbriefje dat nuttig is voor elke amateur-astronoom. Het zal je helpen bij je waarnemingen.
- Grens met het blote oog (kometen): 4
- Grens met het blote oog (planeten en sterren): 6,0
- Grens met 7×50 verrekijker: 9,5
- Grens met telescoop van 35 mm: 11,0
- Grens met telescoop van 60 mm: 12,0
- Grens met telescoop van 102 mm: 13,0
Let op dat lichtvervuiling een enorme invloed heeft op het bereik van magnitudes die je kunt zien! We hebben cijfers gegeven voor observatieomstandigheden dicht bij ideaal, maar ze kunnen verschillen voor jouw locatie. Leer hoe je kunt aangeven hoe donker of helder jouw hemel is met onze handige schaal.

Overigens, om de beperkende magnitude van je telescoop te vinden (de zwakste magnitude die je ermee kunt zien onder perfecte omstandigheden), kun je de Telescoop Beperkende Magnitude Calculator gebruiken.
Conclusie
Magnitude is een van de belangrijkste concepten in observationele astronomie omdat het antwoord geeft op een van de belangrijkste vragen: "Hoe helder is dit object?". Om objecten te classificeren op basis van helderheid, gebruiken astronomen de logaritmische magnitudeschaal, waarbij de helderste objecten de laagste waarden hebben. Door magnitudes te begrijpen, kunnen amateurwaarnemers hun vermogen verbeteren om de helderheid van hemellichamen te identificeren en te vergelijken.
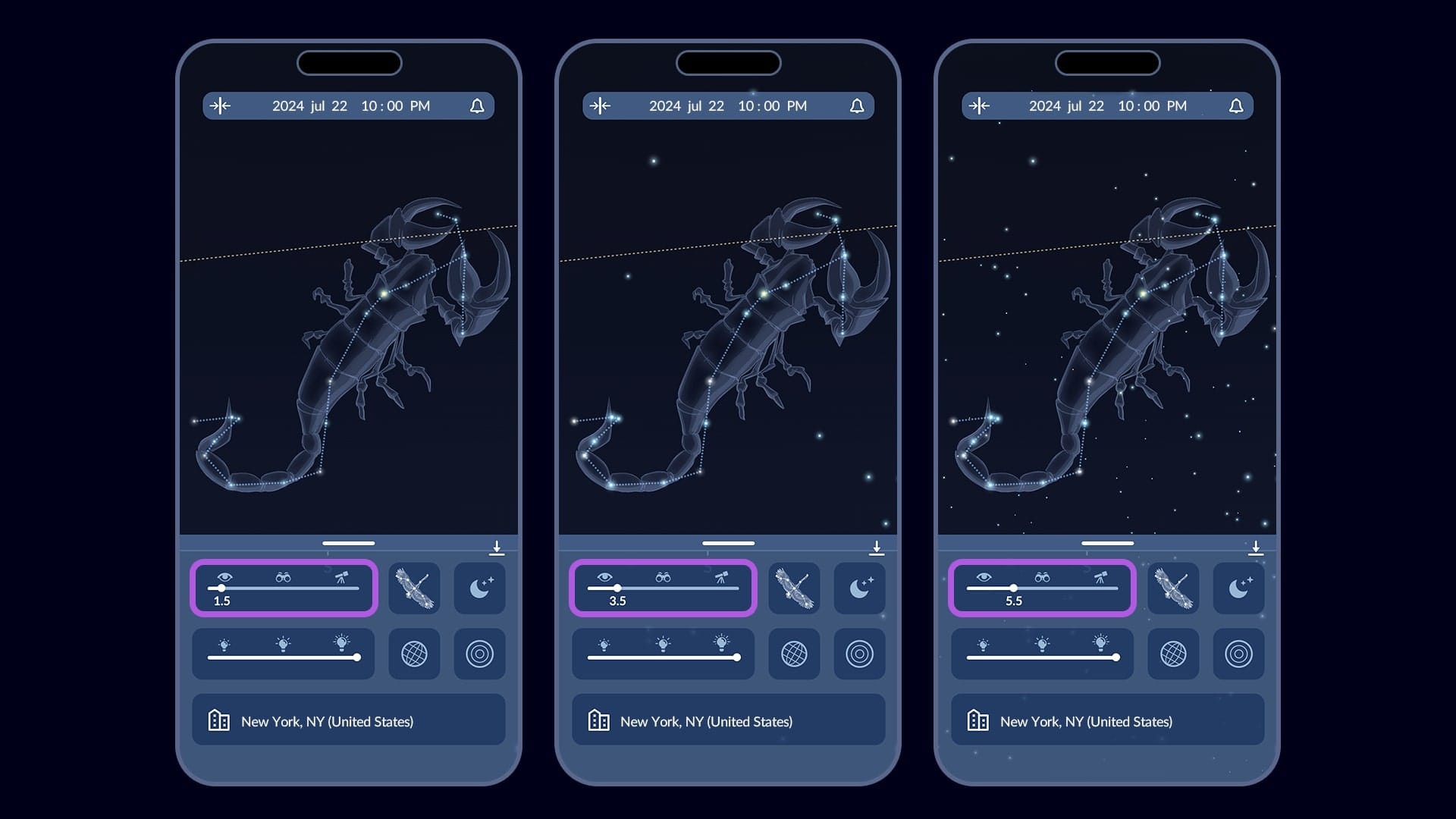
Zie de zwakste objecten aan de hemel met de gratis Sky Tonight app — deze stelt je in staat de magnitudelimiet van wat op je scherm wordt weergegeven te veranderen. Filter objecten op zichtbaarheid met één tik — gebruik iconen voor het blote oog, verrekijkers of telescoop, afhankelijk van je uitrusting.