Magnitude en astronomie : comment la luminosité des astres est-elle mesurée
En connaissant la luminosité d'un objet céleste, vous pouvez déterminer si cet objet est visible ou non. Mais comment mesurez-vous réellement cette luminosité ? Quelle mesure est utilisée dans quel cas ? Clarifions tout cela pour que vous puissiez observer le ciel nocturne comme un pro ! P.S. Pour découvrir rapidement la luminosité de n'importe quel objet dans le ciel, téléchargez l'application Sky Tonight.
Contenu
- Qu'est-ce que la magnitude ?
- Comment la magnitude est-elle mesurée
- Luminosité de surface
- Limites des magnitudes apparentes : guide pour les observateurs
- Conclusion
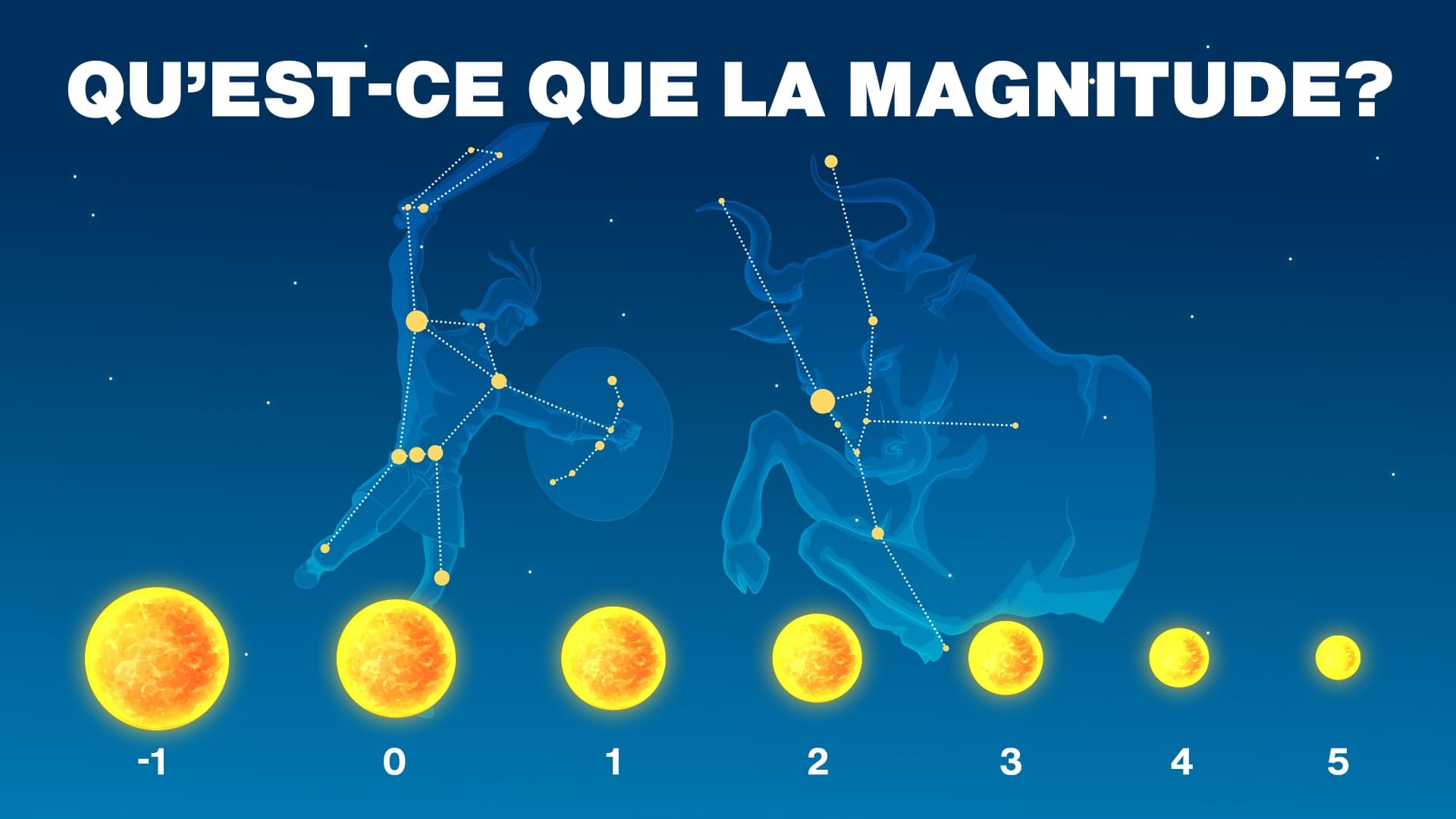
Qu'est-ce que la magnitude ?
En astronomie, la magnitude est une mesure de la luminosité ou de la faiblesse perçue d'un objet dans le ciel.
Remarquez que nous avons utilisé le mot « apparaît » dans la définition. C’est parce que la magnitude, telle qu’on l’emploie habituellement, n’indique pas à quel point un objet est réellement brillant, mais à quel point il semble brillant pour un observateur.
Il ne faut jamais confondre la magnitude avec la luminosité (L) — la puissance totale de la lumière qu’un objet émet dans toutes les directions chaque seconde.
Remarque : Lorsqu’un astronome parle de la brillance d’un objet, il précise généralement la partie du spectre lumineux qu’il mesure. La lumière peut être divisée en différentes régions selon la longueur d’onde — par exemple, ultraviolet (courte), bleue ou visible (ce que nos yeux perçoivent). Pour garantir des mesures cohérentes, les astronomes utilisent des filtres standards qui isolent ces longueurs d’onde, connus sous le nom de bandes U, B et V (ultraviolet, bleue et visible). La bande V correspond à peu près à la sensibilité de l’œil humain et est la plus couramment utilisée.
Sauf indication contraire, toutes les valeurs de magnitude mentionnées dans cet article se réfèrent à la bande V (visuelle).
Magnitude absolue vs. magnitude apparente
Les astronomes distinguent deux grands types de magnitude : apparente et absolue.
- Magnitude apparente (m, souvent simplement appelée “magnitude” ou mag) désigne la brillance d’un objet céleste tel qu’il est vu depuis la Terre.
- Magnitude absolue (M) indique la brillance qu’aurait l’objet s’il se trouvait à une distance fixe de 10 parsecs¹ de la Terre. Les astronomes ont choisi cette distance car elle correspondait à la moyenne des distances stellaires connues en 1902. Pour les planètes et les petits corps du Système solaire, on utilise le symbole H, représentant la brillance que l’objet aurait s’il se situait à une unité astronomique (UA) du Soleil et de l’observateur, complètement éclairé — c’est-à-dire lorsque le Soleil, l’objet et l’observateur sont parfaitement alignés.
¹Unité de distance en astronomie, 1 parsec équivaut à 3,26 années-lumière ou 3,09 × 10¹³ km.
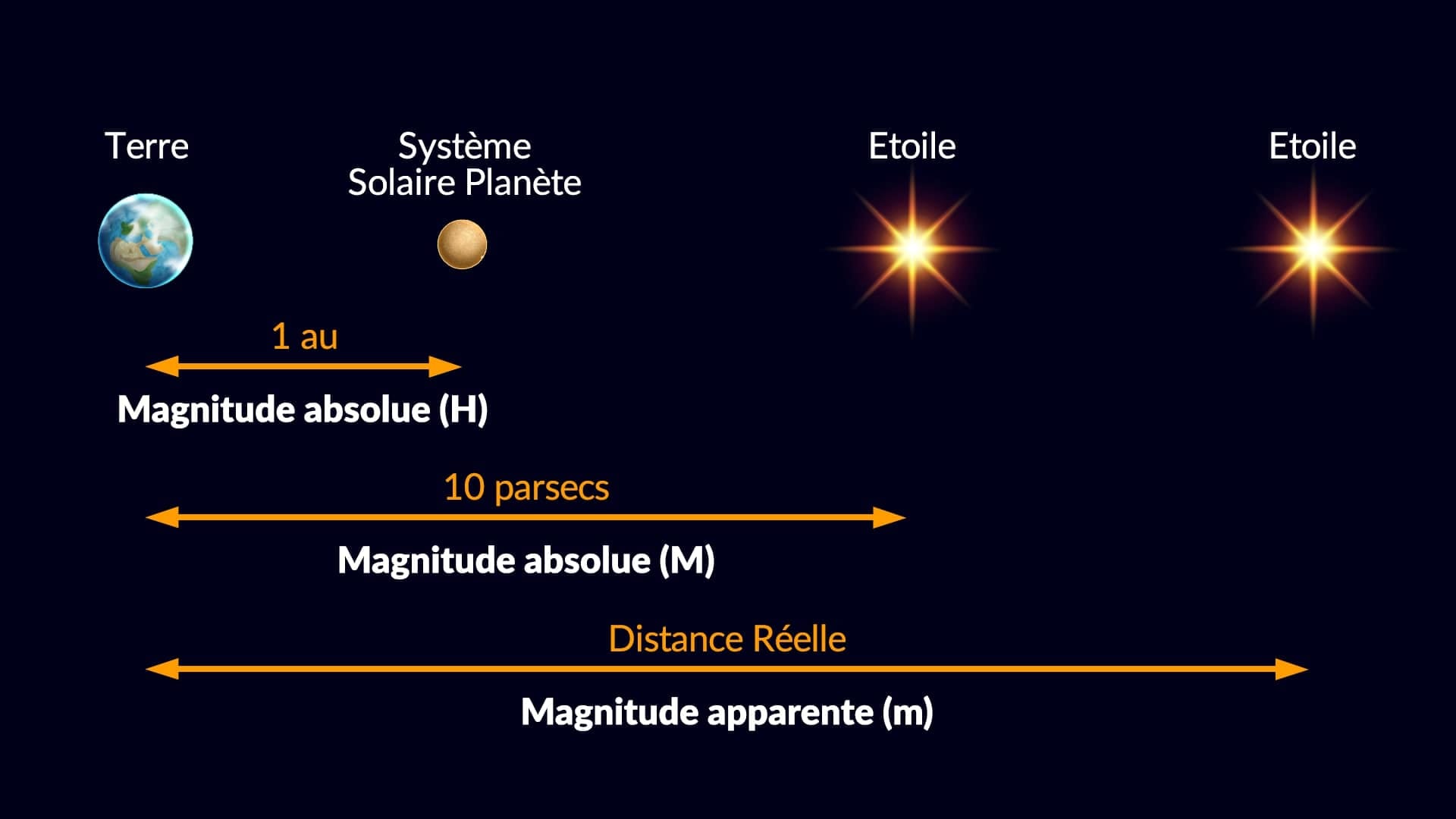
Il est important de souligner que la magnitude absolue d'un objet est mesurée sans extinction (ou assombrissement) de sa lumière due à l'absorption par la matière interstellaire et la poussière cosmique.
Ainsi, la magnitude apparente dépend de la luminosité intrinsèque de l'objet, de sa distance et de l'extinction réduisant sa luminosité. La magnitude absolue nous permet de comparer la luminosité intrinsèque des objets (dans une plage donnée du spectre) en plaçant hypothétiquement tous les objets à une distance de référence standard de l'observateur.
Prenons notre Soleil et Rigel. Le Soleil semble beaucoup plus lumineux que Rigel dans notre ciel, donc sa magnitude apparente est plus élevée (magnitude -26,8 et 0,18 respectivement). Cependant, si nous placions à la fois le Soleil et Rigel à 10 parsecs de la Terre, Rigel éclipserait impressionnament le Soleil. C'est parce que l'étoile lointaine a une magnitude absolue plus élevée : -6,69 contre 4,83 pour le Soleil.
Voici quelques autres exemples :
- Alpha Centauri : m = −0,3 vs M = 4,1
- Canopus : m = −0,7 vs M = −3,1
- Deneb : m = 1,26 vs M = −7,1
- Neptune : m = 7,8 (moy) vs H = −6,9
Les valeurs de magnitude apparente sont exprimées comme un nombre sans unité ; lorsque vous voyez quelque chose comme "Antares a une magnitude de 1,09", cela signifie que la magnitude apparente est sous-entendue. Ceci peut être écrit plus concisément comme "Antares (mag 1,09)", "Antares (1,09 m)" ou "Antares (m = 1,09)". Lorsqu'il s'agit d'autres types de magnitude que l'apparente, les astronomes spécifient le type en écrivant le type de magnitude avec une phrase ou une lettre abréviative : "Antares a une magnitude absolue de −5,28" ou "Antares (M = −5,28)". Ils utilisent également les lettres dans les formules.
D’ailleurs, la magnitude apparente peut être mesurée à l’œil nu ou à l’aide d’instruments, et elle peut concerner n’importe quelle partie du spectre (visible, photographique, ultraviolet, infrarouge, etc.). Dans ce contexte, “apparente” signifie “telle qu’elle est perçue depuis la position de l’observateur, quel que soit l’instrument utilisé”. Lorsqu’il s’agit spécifiquement du rayonnement perçu par l’œil humain, on parle de “magnitude visuelle”. Cependant, de nombreuses sources populaires utilisent ces termes de manière interchangeable, même s’ils ne signifient pas exactement la même chose.
Comment la magnitude est-elle mesurée
Échelle de magnitude
L’échelle de magnitude remonte à l’Antiquité. Des astronomes tels qu’Hipparque (IIᵉ siècle av. J.-C.) et Ptolémée (IIᵉ siècle ap. J.-C.) utilisaient déjà une échelle en six niveaux, allant de un (les plus brillantes) à six (les plus faibles, à peine visibles à l’œil nu).
À l’origine, ce système classait les étoiles en six groupes sans prendre en compte les différences de luminosité à l’intérieur de chaque catégorie. Aujourd’hui, on utilise une version beaucoup plus précise de cette échelle.
Cette ancienne échelle permettait de comparer la brillance apparente des objets célestes les uns aux autres. Un tel système nécessite un point zéro, ou une étoile de référence. Traditionnellement, Vega, avec une magnitude apparente de 0,0, a servi de référence.
Avec l’invention des télescopes, les astronomes ont élargi cette échelle pour inclure des objets beaucoup plus faibles, comme les nébuleuses diffuses et les galaxies lointaines.
Ils ont également étendu l’échelle aux objets plus brillants du ciel, comme le Soleil, la Lune et certaines planètes. Comme Vega était considérée comme l’étoile de magnitude zéro, les objets plus lumineux ont reçu des valeurs négatives. Voici quelques exemples de magnitudes apparentes :
- Soleil : –26,7
- Pleine Lune : –12,7 (moyenne)
- Vénus : jusqu’à –4,8 (selon la phase)
- Jupiter : –2,9 (à l’opposition)
- Sirius : –1,4
- Vega : 0,0
- Deneb : 1,2
Ainsi, cette échelle de magnitude peut être déroutante, mais souvenez-vous simplement que plus le nombre est grand, plus l'objet est sombre. Les objets les plus lumineux ont des magnitudes négatives.

Comment les étoiles sont-elles distribuées par magnitude ?
Vous avez peut-être remarqué qu'il y a beaucoup plus d'étoiles plus sombres que d'étoiles plus lumineuses dans notre ciel nocturne. Voici une répartition simplifiée du nombre d'étoiles par leurs magnitudes :
- Magnitude de –1,5 à –0,5 : 2 étoiles
- Magnitude de –0,5 à 0,5 : 6 étoiles
- Magnitude de 0,5 à 1,5 : 14 étoiles
- Magnitude de 1,5 à 2,5 : 71 étoiles
- Magnitude de 2,5 à 3,5 : 190 étoiles
- Magnitude de 3,5 à 4,5 : 610 étoiles
- Magnitude de 4,5 à 5,5 : 1 929 étoiles
- Magnitude de 5,5 à 6,5 : 5 946 étoiles
Notez que ces nombres représentent toutes les étoiles visibles à l'œil nu dans l'ensemble du ciel. Puisque nous ne pouvons voir que la moitié du ciel à un moment donné, le nombre réel d'étoiles que vous pouvez voir en une fois est différent.
Comment l'échelle de magnitude apparente est-elle calculée ?
Nous savons qu'une étoile de magnitude 1 est plus lumineuse qu'une étoile de magnitude 2. Mais de combien ?
L'échelle de magnitude est logarithmique, où une différence de 5 magnitudes correspond toujours à un changement de luminosité par un facteur de 100. Cela signifie qu'une étoile de magnitude 1 est 100 fois plus lumineuse qu'une étoile de magnitude 6, et de même, une étoile de magnitude 2 est 100 fois plus lumineuse qu'une étoile de magnitude 7.
Voici comment fonctionne l'échelle :
- Une différence d'une magnitude (comme de 1 à 2) change la luminosité d'environ 2,5 fois.
- Ce facteur se cumule à chaque étape, ce qui signifie qu'une étoile de magnitude 3 est 6,25 fois plus sombre qu'une étoile de magnitude 1 (2,5 x 2,5 = 6,25).
Si nous étendons cette échelle à cinq magnitudes, le facteur devient 2,5, élevé à la cinquième puissance, soit environ 100. Mais si vous utilisez une calculatrice, vous verrez que les chiffres ne correspondent pas exactement. C'est parce que 2,5 est une simplification ; le nombre précis est 100^(1/5) ≈ 2,51188643150958. Dans la plupart des sources, vous verrez ce nombre raccourci à 2,5 ou 2,512. Voici le changement de magnitude entre les étoiles avec des différences de 1, 2, 3, 4 et 5 magnitudes :
- Différence de 1 magnitude : 2,512 ≈ 2,5
- Différence de 2 magnitudes : 2,512 x 2,512 ≈ 6,3
- Différence de 3 magnitudes : 2,512 x 2,512 x 2,512 ≈ 15,8
- Différence de 4 magnitudes : 2,512 x 2,512 x 2,512 x 2,512 ≈ 39,8
- Différence de 5 magnitudes : 2,512 x 2,512 x 2,512 x 2,512 x 2,512 ≈ 100
Maintenant, nous pouvons calculer à quel point la Pleine Lune est plus lumineuse que Vénus, l'objet le plus lumineux suivant dans le ciel nocturne. Leurs magnitudes varient légèrement, prenons donc les magnitudes –12,7 pour la Pleine Lune et –4,6 pour Vénus.
La différence de magnitudes entre la Pleine Lune et Vénus est de –4,6 – (–12,7) = 8,1 unités.
Une différence de magnitude de 1 augmente la luminosité d'environ 2,512 fois, donc une augmentation de magnitude de 8,1 fois augmentera la luminosité de (2,512)^8.1 fois, soit ≈1 700.
Ainsi, la Pleine Lune est environ 1 700 fois plus lumineuse que Vénus ! Si nous utilisons l'équation générale pour comparer la luminosité basée sur les magnitudes, cela peut être exprimé comme suit :
Iᴬ / Iᴮ ≈ 2.512^(mᴮ – mᴬ)
Ici Iᴬ et Iᴮ représentent les intensités (ou luminosités) des objets A et B, respectivement, et mᴮ, mᴬ sont leurs magnitudes.
Comment trouver la magnitude apparente ?
Pour déterminer la magnitude apparente précise d'un objet, les astronomes mesurent le flux ou l'intensité de cet objet (la quantité totale d'énergie par unité de surface arrivant sur le détecteur du télescope par seconde). Ensuite, ils comparent à quel point la source semble lumineuse en la comparant avec l'étoile de référence, en utilisant la formule suivante :
m₁ – m₀ = –2.5 × log₁₀ (F₁ / F₀)
où m représente la magnitude (comme nous le savons déjà) et F le flux. I est utilisé au lieu de F dans de nombreuses sources, car les astronomes utilisent le terme "flux" pour ce qui est souvent appelé "intensité" en physique.
Comme nous l'avons déjà mentionné, l'étoile de référence (le point zéro) a été choisie comme étant l'étoile Véga (c'est-à-dire que F₀ est le flux de Véga, et m₀ est la magnitude de Véga).
Avec l’arrivée de photomètres et de caméras de grande précision, les astronomes ont découvert que même Vega n’était pas une référence parfaite, sa brillance variant légèrement (≈ 0,03 magnitudes). Pour garantir la cohérence entre différentes bandes de longueurs d’onde, le point zéro a ensuite été défini à partir d’une source constante théorique plutôt que d’une étoile réelle. Cependant, pour les observations visuelles, Vega reste la référence standard de magnitude zéro.
Il existe toute une branche de la science dédiée à la mesure de la luminosité des étoiles et d'autres objets célestes — la photométrie.
Différents systèmes de magnitude : gammes spectrales
La magnitude dépend de la sensibilité spectrale du récepteur (œil, détecteur photoélectrique, plaque photographique, etc.).
Il existe de nombreux systèmes de magnitudes par rapport aux gammes spectrales, chacun différant dans le choix d'une gamme de mesure particulière.
Magnitude visuelle (mᵥ) décrit l'apparence d'une étoile à l'œil.
Magnitude photographique (mₚ) est mesurée à partir d'une image d'une étoile sur une plaque photographique obtenue sans filtres de lumière supplémentaires. Étant donné que l'émulsion photo est sensible aux rayons bleus et insensible aux rayons rouges, les étoiles bleues apparaissent plus lumineuses (que ce qu'elles semblent à l'œil) sur la plaque photographique.
En comparant les luminosités d'une source mesurées dans différentes bandes du spectre, les astronomes peuvent connaître sa couleur, estimer sa température de surface (si c'est une étoile) ou l'albédo (si c'est une planète), déterminer le degré d'absorption de la lumière interstellaire, et d'autres caractéristiques importantes.
Ainsi, des systèmes photométriques standard, principalement déterminés par le choix des filtres de lumière, ont été développés. Le plus populaire est le système à trois couleurs UBV : ultraviolet (U), bleu (B) et visuel (V). La gamme visuelle est très proche de la gamme photovisuelle, et la gamme bleue est proche de la gamme photographique.
En plus des récepteurs sensibles aux spectres, il existe des bolomètres qui mesurent la magnitude bolométrique — le flux de rayonnement cumulé sur toutes les gammes du spectre. La magnitude bolométrique permet de calculer la luminosité d'un objet si la distance à la source et le degré d'absorption interstellaire sont connus.
Luminosité de surface
Jusqu'à présent, nous avons principalement discuté de sources de lumière ponctuelles, telles que les étoiles et les planètes. Mais tous les objets dans le ciel nocturne ne sont pas aussi compacts que les étoiles.
Certains objets célestes s'étendent sur une vaste zone, comme les galaxies et les nébuleuses. Prendre tout le flux lumineux d'un objet et en déterminer une magnitude peut être trompeur.
Dans ce cas, la magnitude apparente ne répond pas vraiment à la question principale : à quel point cet objet est-il lumineux pour l'observateur sur Terre ?
Par exemple, la Galaxie d'Andromède a une magnitude apparente de 3,4, ce qui devrait être visible à l'œil nu même dans une zone polluée par la lumière ! Cependant, cela ne correspond pas à ce que nous voyons dans le ciel nocturne.

Les astronomes abordent ce problème en utilisant la luminosité de surface, une mesure de la luminosité par unité de surface. Cela moyenne la luminosité de l'objet sur l'ensemble de l'objet.
Luminosité de surface (SB) quantifie la luminosité apparente ou la densité de flux par unité de surface angulaire d'un objet spatial étendu tel qu'une galaxie ou une nébuleuse ou du fond du ciel nocturne.
La luminosité de surface d'un objet est souvent exprimée soit en magnitudes par seconde d'arc carré (mag/arcsec²) soit en magnitudes par minute d'arc carré (mag/arcmin²). Voici quelques objets avec la magnitude apparente et la luminosité de surface la plus faible (la plus lumineuse) :
- Nébuleuse d'Orion : 4 m vs 17 mag/arcsec²
- Galaxie d'Andromède : 3,4 m vs 11 mag/arcsec²
- Galaxie du Triangle : 5,7 m vs 14,2 mag/arcsec²
- Galaxie de Bode : 6,9 m vs 25 mag/arcsec²
Cependant, la luminosité de surface d'un objet est rarement mentionnée, bien qu'elle soit importante pour les observations visuelles.

Fait intéressant : les yeux détectent mieux la lumière d'une source diffuse, ou étendue, (comme les galaxies) que d'une source ponctuelle (comme une étoile).
Cela signifie qu'il est plus facile de voir des objets avec une luminosité diffuse que des objets avec une source ponctuelle. Le noyau de la Galaxie d'Andromède est à ~11 mag/arcsec² mais est encore visible à l'œil. Le bord extérieur de la galaxie peut être vu avec des télescopes à 22 mag/arcsec², une cible beaucoup plus sombre !
Limites des magnitudes apparentes : guide pour les observateurs
La magnitude limite est la magnitude apparente de l'objet le plus faible visible dans le ciel. Voici une feuille de triche utile pour tout astronome amateur. Elle vous aidera dans vos observations.
- Limite à l’œil nu (comètes) : 4
- Limite à l’œil nu (planètes et étoiles) : 6,0
- Limite avec jumelles 7×50 : 9,5
- Limite avec télescope de 35 mm : 11,0
- Limite avec télescope de 60 mm : 12,0
- Limite avec télescope de 102 mm : 13,0
Notez que la pollution lumineuse a un énorme effet sur la gamme de magnitudes que vous pouvez voir ! Nous avons fourni des chiffres pour des conditions d'observation proches de l'idéal, mais ils peuvent être différents pour votre localisation. Apprenez à indiquer à quel point votre ciel est sombre ou lumineux avec notre échelle pratique.

Au fait, pour trouver la magnitude limite de votre télescope (la magnitude la plus faible que vous pouvez voir avec sous des conditions parfaites), vous pouvez utiliser le Calculateur de magnitude limite du télescope.
Conclusion
La magnitude est l'un des concepts les plus importants en astronomie observationnelle car elle répond à l'une des questions les plus importantes : "Quelle est la luminosité de cet objet ?". Pour classer les objets par luminosité, les astronomes utilisent l'échelle de magnitude logarithmique, où les objets les plus lumineux ont les valeurs les plus basses. En comprenant les magnitudes, les observateurs amateurs peuvent améliorer leur capacité à identifier et comparer la luminosité des objets célestes.
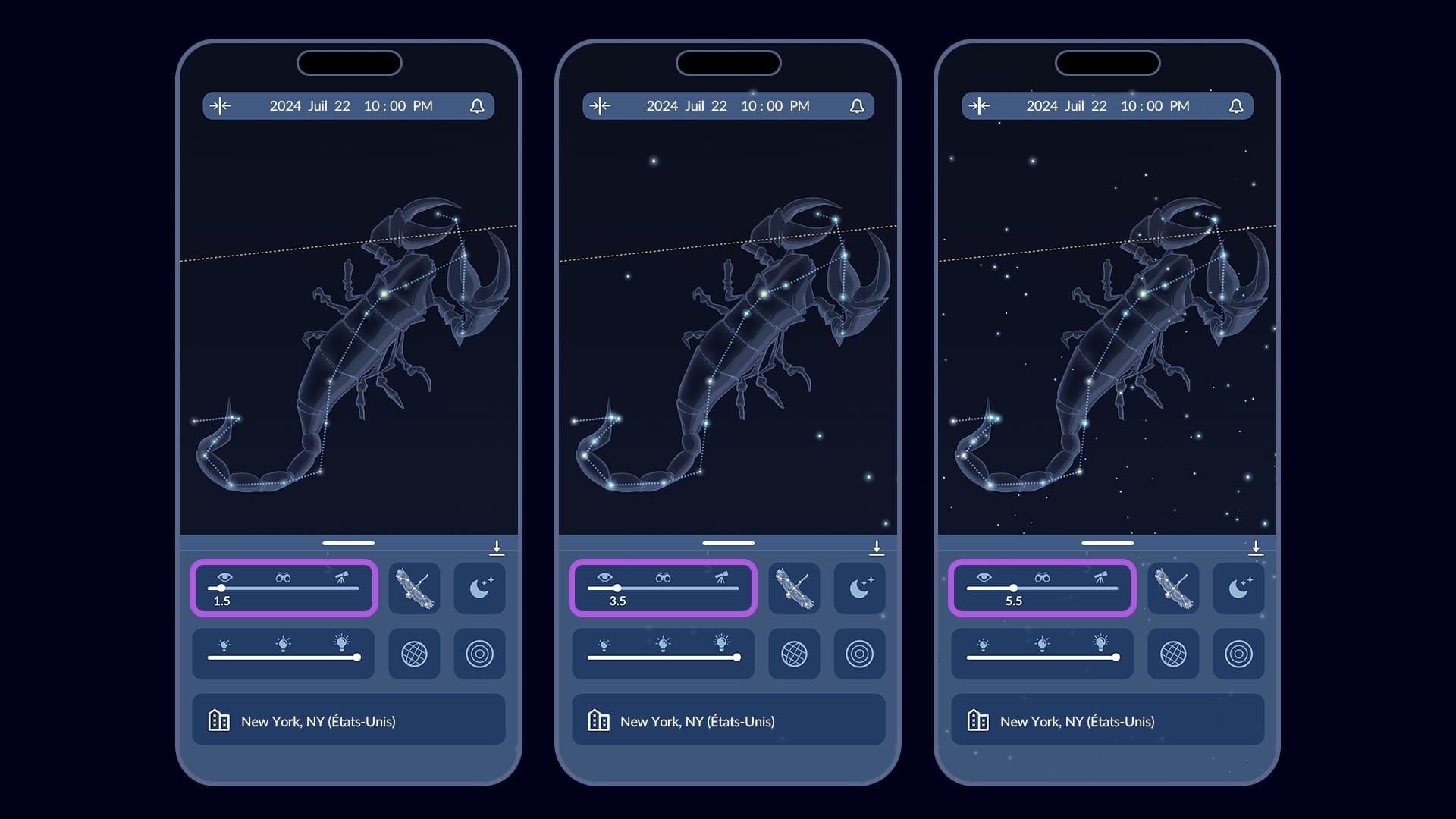
Voyez les objets les plus faibles dans le ciel avec l'application gratuite Sky Tonight — elle vous permet de changer la limite de magnitude de ce qui est affiché sur votre écran. Filtrez les objets par visibilité en un clic — utilisez des icônes pour l'œil nu, les jumelles ou le télescope en fonction de votre équipement.