Magnitud en astronomía: cómo se mide el brillo de los astros
Al conocer el brillo de un objeto celestial, puedes saber si este objeto es visible o no. Pero, ¿cómo se mide realmente este brillo? ¿Qué medición se utiliza en qué caso? ¡Aclarémoslo todo para que puedas observar el cielo nocturno como un profesional! P.D. Para encontrar rápidamente el brillo de cualquier objeto en el cielo, obtén la aplicación Sky Tonight.
Contenido
- ¿Qué es la magnitud?
- ¿Cómo se mide la magnitud?
- Brillo superficial
- Magnitudes aparentes límite: guía para observadores
- Conclusión
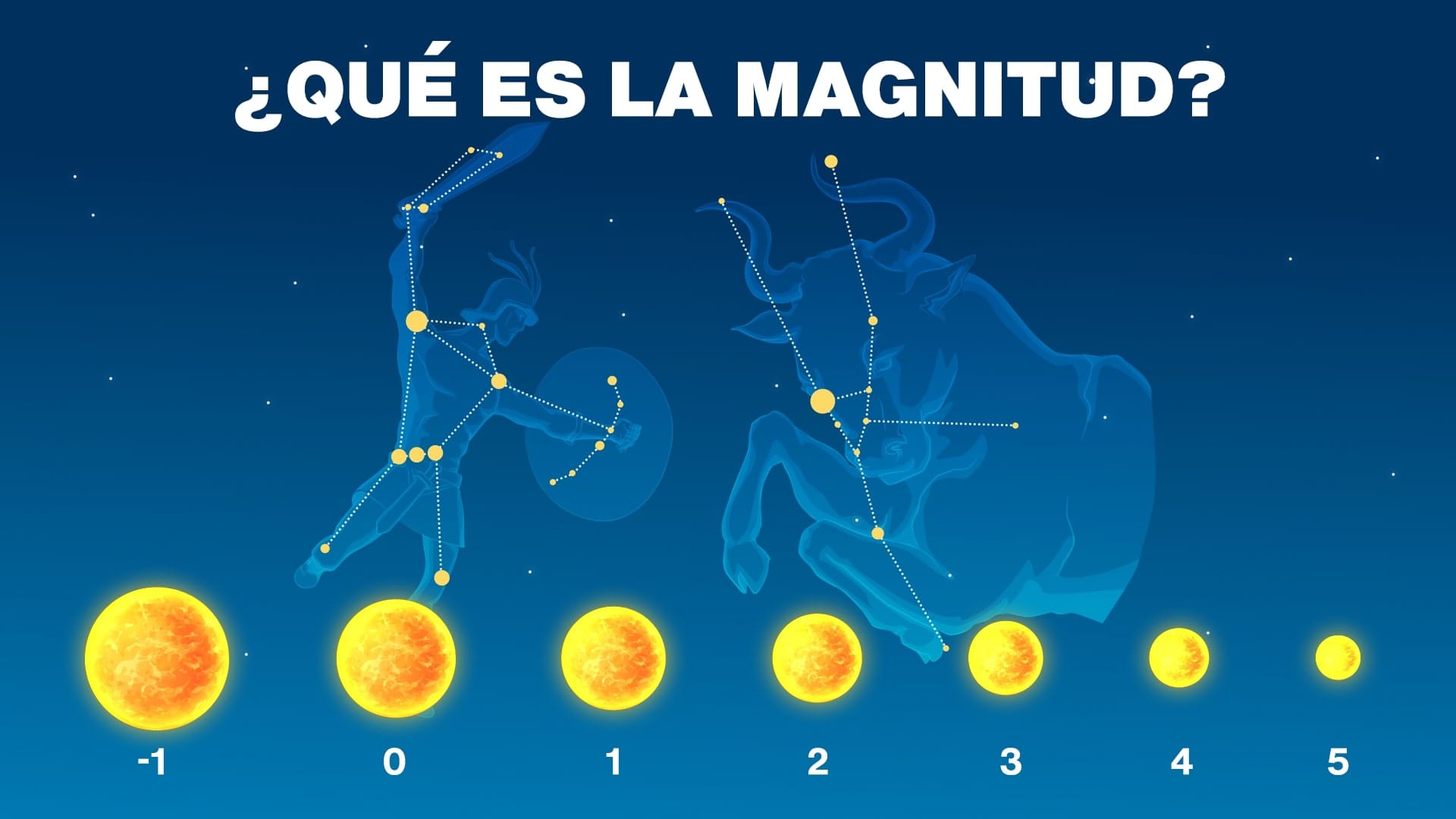
¿Qué es la magnitud?
En astronomía, la magnitud es una medida de cuán brillante o tenue parece un objeto en el cielo.
Observa que usamos el término “parece” en la definición. Esto se debe a que la magnitud, tal como se entiende habitualmente, no indica cuán brillante es realmente un objeto, sino cuán brillante parece para un observador.
No debes confundir nunca la magnitud con la luminosidad (L): la potencia total de la luz que un objeto emite en todas las direcciones cada segundo.
Nota: Cuando los astrónomos hablan del brillo de un objeto, normalmente especifican qué parte del espectro de luz están midiendo. La luz puede dividirse en diferentes regiones según su longitud de onda. Por ejemplo: ultravioleta (longitud de onda corta), azul o visual (lo que nuestros ojos pueden ver). Para garantizar mediciones coherentes, los astrónomos utilizan filtros estándar que aíslan esas longitudes de onda, conocidos como bandas U, B y V (ultravioleta, azul y visual). La banda V corresponde aproximadamente a la sensibilidad del ojo humano y es la más utilizada.
A menos que se indique lo contrario, todos los valores de magnitud mencionados en este artículo se refieren a la banda V (visual).
Magnitud absoluta vs. magnitud aparente
Los astrónomos dividen la magnitud en dos tipos generales: aparente y absoluta.
- Magnitud aparente (m, a menudo simplemente “magnitud” o mag) es el brillo de un objeto celeste tal como se ve desde la Tierra.
- Magnitud absoluta (M) es el brillo que tendría un objeto si estuviera a una distancia fija de 10 pársecs¹ de la Tierra. Parece que los astrónomos eligieron esta distancia porque era cercana al promedio de las distancias estelares conocidas en 1902. Para los planetas y cuerpos menores del Sistema Solar, se usa el símbolo H, que representa el brillo que tendría un objeto si se encontrara a una unidad astronómica (UA) tanto del Sol como del observador y estuviera completamente iluminado, es decir, con el Sol, el objeto y el observador perfectamente alineados.
¹Una unidad de distancia en astronomía, 1 parsec equivale a 3.26 años luz o 3.09 × 10¹³ km.
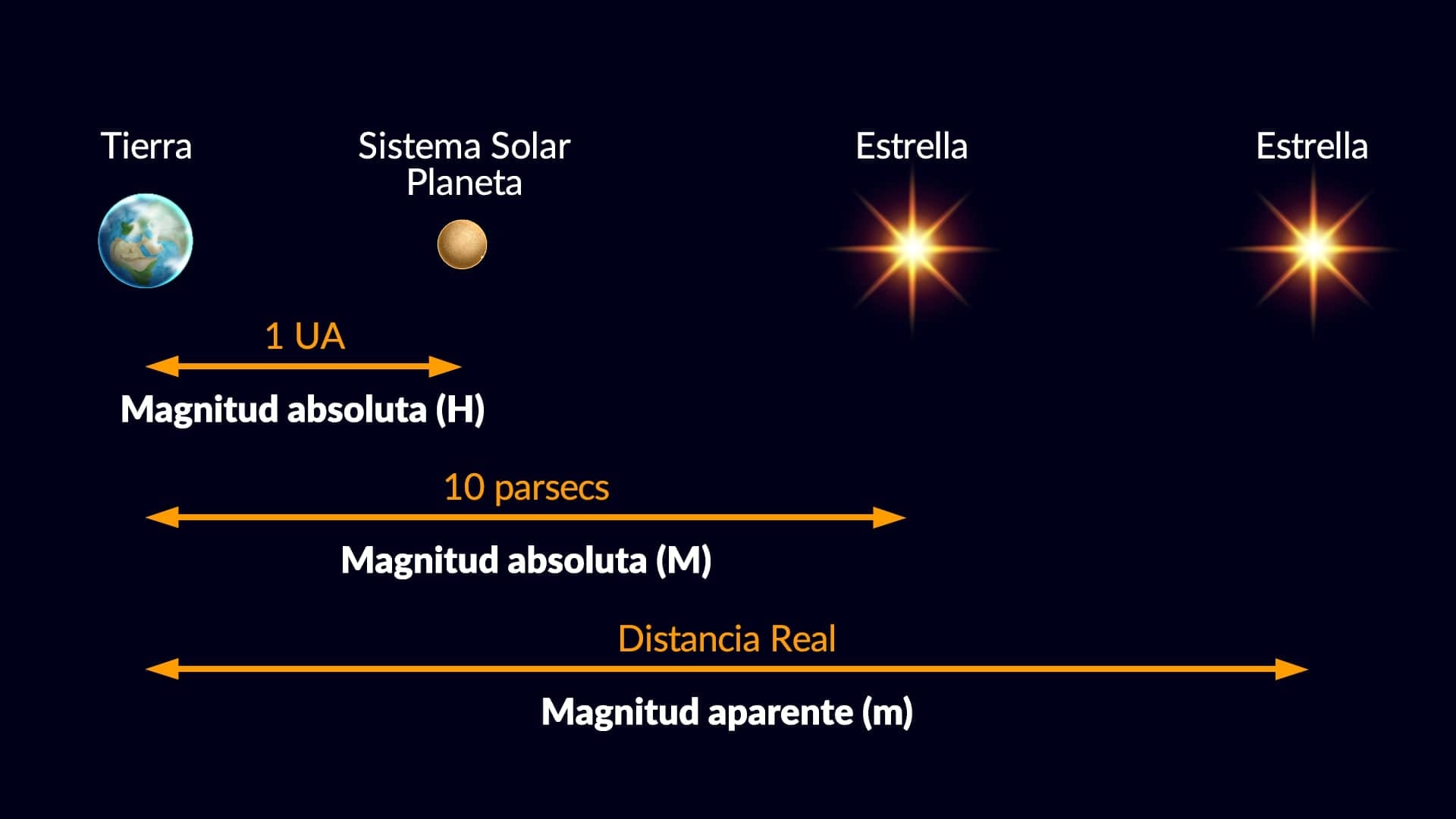
Es importante señalar que la magnitud absoluta de un objeto se mide sin la extinción (o atenuación) de su luz debido a la absorción por parte de la materia interestelar y el polvo cósmico.
Así que la magnitud aparente depende de la luminosidad intrínseca de un objeto, su distancia y la extinción que reduce su brillo. La magnitud absoluta nos permite comparar la luminosidad intrínseca de los objetos (en un rango dado del espectro) colocando hipotéticamente a todos los objetos a una distancia estándar de referencia del observador.
Tomemos nuestro Sol y Rigel. El Sol aparece mucho más brillante que Rigel en nuestro cielo, por lo que su magnitud aparente es más alta (magnitud −26.7 y 0.13, respectivamente). Sin embargo, si colocáramos tanto el Sol como a Rigel a 10 parsecs de la Tierra, Rigel impresionantemente superaría en brillo al Sol. Esto se debe a que la estrella distante tiene una magnitud absoluta más alta: -6.69 frente a 4.83 para el Sol.
Aquí hay algunos ejemplos más:
- Alfa Centauri: m = −0.3 vs M = 4.1
- Canopus: m = −0.7 vs M = −3.1
- Deneb: m = 1.26 vs M = −7.1
- Neptuno: m = 7.8 (promedio) vs H = −6.9
Los valores de magnitud aparente se expresan como un número sin unidad; cuando ves algo como "Antares tiene una magnitud de 1.09", significa que se está implicando la magnitud aparente. Esto se puede escribir de forma más concisa como "Antares (mag 1.09)", "Antares (1.09 m)" o "Antares (m = 1.09)". Cuando se refieren a tipos de magnitud distintos de la aparente, los astrónomos especifican el tipo escribiendo el tipo de magnitud con una frase o letra de abreviación: "Antares tiene una magnitud absoluta de −5.28" o "Antares (M = −5.28)". También usan las letras en fórmulas.
Por cierto, la magnitud aparente puede medirse tanto a simple vista como con instrumentos, y puede referirse al brillo en cualquier rango del espectro (visual, fotográfico, ultravioleta, infrarrojo, etc.). En este contexto, “aparente” significa “tal como se ve desde la posición del observador, independientemente del instrumento utilizado”. Cuando nos referimos específicamente al brillo percibido por el ojo humano, usamos el término “magnitud visual”. Sin embargo, muchas fuentes populares utilizan estos términos indistintamente, aunque no sean exactamente lo mismo.
¿Cómo se mide la magnitud?
Escala de magnitud
La escala de magnitud tiene una larga historia. Astrónomos antiguos como Hiparco (siglo II a. C.) y Ptolomeo (siglo II d. C.) la usaron para clasificar las estrellas en una escala de seis grados, del uno (más brillante) al seis (más débil y apenas visible a simple vista).
Inicialmente, este sistema dividía las estrellas en seis grupos, pero no consideraba las diferencias de brillo dentro de cada grupo. Hoy en día, utilizamos una versión más refinada de esa escala.
Esa antigua escala es un sistema para determinar cuán brillantes parecen los objetos celestes en comparación unos con otros. Dicho sistema requiere un punto cero o una estrella de referencia. Tradicionalmente, Vega, con una magnitud aparente de 0,0, fue tomada como esa referencia.
Con el desarrollo de los telescopios, los astrónomos ampliaron la escala para incluir objetos mucho más débiles, como nebulosas y galaxias lejanas.
También extendieron la escala para cubrir objetos más brillantes del cielo, como el Sol, la Luna y algunos planetas. Como Vega se consideraba la estrella de magnitud cero, a los objetos más brillantes se les asignaron valores negativos. Aquí algunos ejemplos de magnitudes aparentes:
- Sol: –26,7
- Luna llena: –12,7 (promedio)
- Venus: hasta –4,8 (según su fase)
- Júpiter: –2,9 (en oposición)
- Sirio: –1,4
- Vega: 0,0
- Deneb: 1,2

¿Cómo se distribuyen las estrellas por magnitud?
Podrías haber notado que hay muchas más estrellas tenues que brillantes en nuestro cielo nocturno. Aquí tienes un desglose simplificado del número de estrellas por sus magnitudes:
- Magnitud de –1.5 a –0.5: 2 estrellas
- Magnitud de –0.5 a 0.5: 6 estrellas
- Magnitud de 0.5 a 1.5: 14 estrellas
- Magnitud de 1.5 a 2.5: 71 estrellas
- Magnitud de 2.5 a 3.5: 190 estrellas
- Magnitud de 3.5 a 4.5: 610 estrellas
- Magnitud de 4.5 a 5.5: 1,929 estrellas
- Magnitud de 5.5 a 6.5: 5,946 estrellas
Nota que estos números representan todas las estrellas visibles a simple vista en todo el cielo. Dado que solo podemos ver la mitad del cielo en cualquier momento, el número real de estrellas que puedes ver al mismo tiempo es diferente.
¿Cómo se calcula la escala de magnitud aparente?
Sabemos que una estrella de magnitud 1 es más brillante que una estrella de magnitud 2. Pero, ¿cuánto más brillante?
La escala de magnitud es logarítmica, donde una diferencia de 5 magnitudes siempre corresponde a un cambio de brillo por un factor de 100. Esto significa que una estrella de magnitud 1 es 100 veces más brillante que una estrella de magnitud 6, y de manera similar, una estrella de magnitud 2 es 100 veces más brillante que una estrella de magnitud 7.
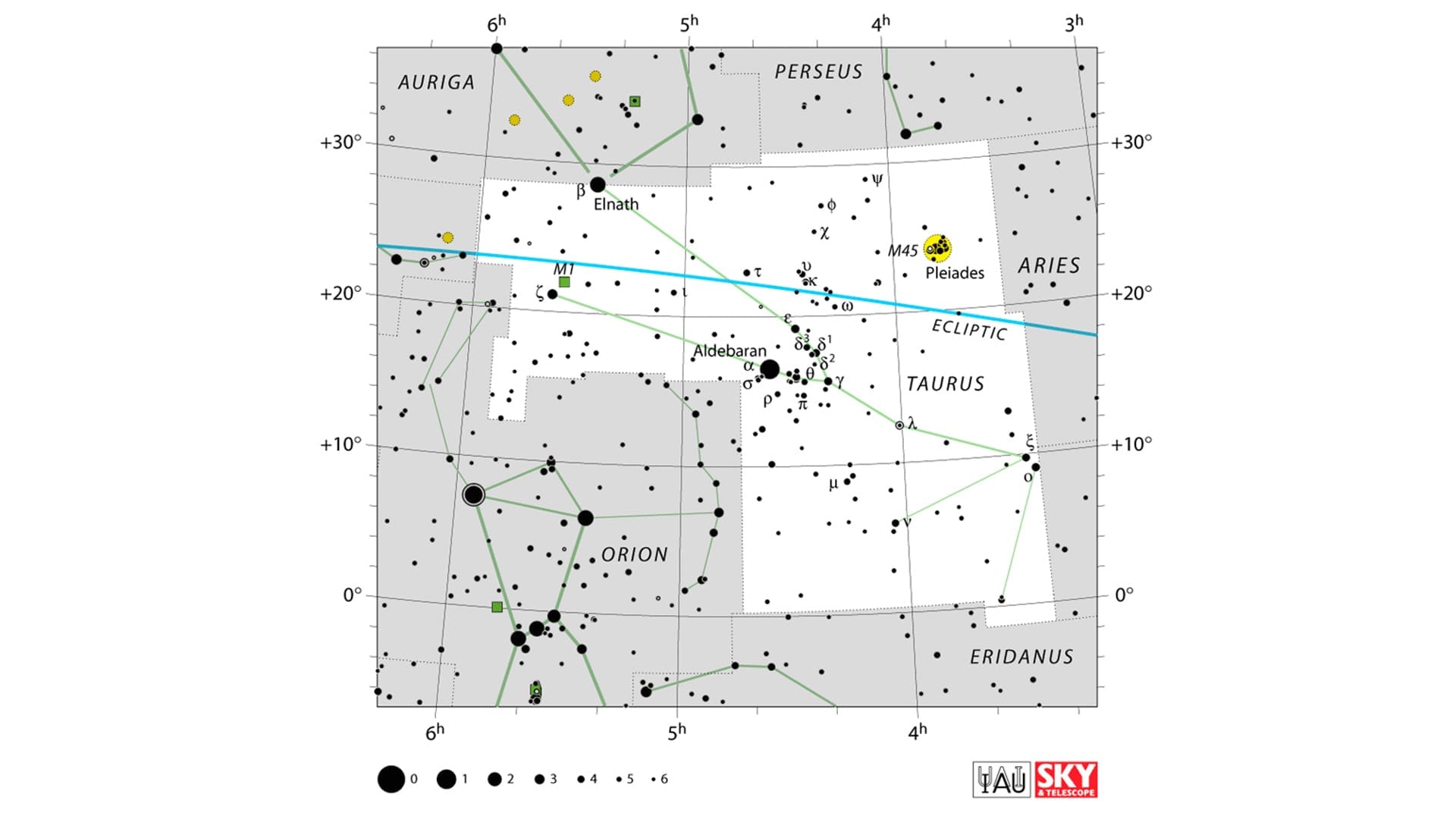
Así es como funciona la escala:
- Una diferencia de magnitud de uno (como de 1 a 2) cambia el brillo aproximadamente 2.5 veces.
- Este factor se compone con cada paso, lo que significa que una estrella de magnitud 3 es 6.25 veces más tenue que una estrella de magnitud 1 (2.5 x 2.5 = 6.25).
Si extendemos esta escala a cinco magnitudes, el factor se convierte en 2.5, elevado a la quinta potencia, que es aproximadamente 100. Pero si usas una calculadora, verás que los números no coinciden exactamente. Eso es porque 2.5 es una simplificación; el número preciso es 100^(1/5) ≈ 2.51188643150958. En la mayoría de las fuentes, verás este número acortado a 2.5 o 2.512. Aquí está el cambio en magnitud entre estrellas con diferencias de 1, 2, 3, 4 y 5 magnitudes:
- Diferencia de 1 magnitud: 2.512 ≈ 2.5
- Diferencia de 2 magnitudes: 2.512 x 2.512 ≈ 6.3
- Diferencia de 3 magnitudes: 2.512 x 2.512 x 2.512 ≈ 15.8
- Diferencia de 4 magnitudes: 2.512 x 2.512 x 2.512 x 2.512 ≈ 39.8
- Diferencia de 5 magnitudes: 2.512 x 2.512 x 2.512 x 2.512 x 2.512 ≈ 100
Ahora, podemos calcular cuánto más brillante es la Luna Llena en comparación con Venus, el siguiente objeto más brillante en el cielo nocturno. Sus magnitudes varían ligeramente, así que tomemos magnitudes –12.7 para la Luna Llena y –4.6 para Venus.
La diferencia en magnitudes de la Luna Llena y Venus es –4.6 – (–12.7) = 8.1 unidades.
Una diferencia en magnitud de 1 aumenta el brillo aproximadamente 2.512 veces, por lo que un aumento en magnitud de 8.1 veces aumentará el brillo por (2.512)^8.1 veces, lo que es ≈1,700.
¡Así que la Luna Llena es aproximadamente 1,700 veces más brillante que Venus! Si usamos la ecuación general para comparar el brillo basado en magnitudes, se puede expresar como:
Iᴬ / Iᴮ ≈ 2.512^(mᴮ – mᴬ)
¿Cómo encontrar la magnitud aparente?
Para encontrar la magnitud aparente precisa de un objeto, los astrónomos miden el flujo o intensidad de este objeto (la cantidad total de energía por unidad de área que llega al detector del telescopio por segundo). Luego, comparan cuán brillante parece ser la fuente comparándola con la estrella de referencia, usando la siguiente fórmula:
m₁ – m₀ = –2.5 × log₁₀ (F₁ / F₀)
donde m es la magnitud (como ya sabemos) y F es el flujo. En muchas fuentes, se usa I en lugar de F, ya que los astrónomos usan el término "flujo" para lo que a menudo se llama "intensidad" en física.
Como ya mencionamos, la estrella de referencia (el punto cero) se eligió como la estrella Vega (es decir, F₀ es el flujo de Vega, y m₀ es la magnitud de Vega).
Con la llegada de fotómetros y cámaras de alta precisión, los astrónomos descubrieron que incluso Vega no era una referencia perfecta, ya que su brillo puede variar ligeramente (≈0,03 magnitudes). Para garantizar la coherencia entre diferentes longitudes de onda, se definió el punto cero utilizando una fuente constante idealizada en lugar de una estrella real. Sin embargo, para observaciones visuales, Vega sigue siendo el estándar de magnitud cero.
Existe toda una rama de la ciencia dedicada a la medición del brillo de las estrellas y otros objetos celestes: la fotometría.
Diferentes sistemas de magnitud: rangos espectrales
La magnitud depende de la sensibilidad espectral del receptor (ojo, detector fotoeléctrico, placa fotográfica, etc.).
Existen muchos sistemas de magnitudes con respecto a rangos espectrales, cada uno difiriendo en la elección de un rango de medición particular.
Magnitud visual (mᵥ) describe cómo se ve una estrella a simple vista.
Magnitud fotográfica (mₚ) se mide a partir de una imagen de una estrella en una placa fotográfica obtenida sin filtros de luz adicionales. Dado que la emulsión fotográfica es sensible a los rayos azules e insensible a los rayos rojos, las estrellas azules aparecen más brillantes (de lo que parecen al ojo) en la placa fotográfica.
Comparando las luminosidades de una fuente medidas en diferentes bandas del espectro, los astrónomos pueden conocer su color, estimar su temperatura superficial (si es una estrella) o albedo (si es un planeta), determinar el grado de absorción de luz interestelar y otras características importantes.
Por lo tanto, se han desarrollado sistemas estándar de rangos fotométricos, principalmente determinados por la selección de filtros de luz. El más popular es el sistema de tres colores UBV: ultravioleta (U), azul (B) y visual (V). El rango visual está muy cerca del rango fotovisual, y el rango azul está cerca del rango fotográfico.
Además de los receptores sensibles al espectro, hay bolómetros que miden la magnitud bolométrica: el flujo de radiación sumado sobre todos los rangos del espectro. La magnitud bolométrica permite calcular la luminosidad de un objeto si se conoce la distancia a la fuente y el grado de absorción interestelar.
Brillo superficial
Hasta ahora, hemos discutido principalmente fuentes de luz puntuales, como estrellas y planetas. Pero no todos los objetos en el cielo nocturno son tan compactos como las estrellas.
Algunos objetos celestes se extienden sobre una amplia área, como galaxias y nebulosas. Tomar todo el flujo de luz de un objeto y determinar una magnitud a partir de él puede ser engañoso.
Por lo tanto, en este caso, la magnitud aparente realmente no ayuda a responder la pregunta principal: ¿cuán brillante es este objeto para el observador en la Tierra?
Por ejemplo, la Galaxia de Andrómeda tiene una magnitud aparente de 3.4, ¡lo que debería ser visible a simple vista incluso en un área contaminada por luz! Sin embargo, esto no coincide con lo que vemos en el cielo nocturno.

Los astrónomos abordan este problema usando el brillo superficial, una medida del brillo por unidad de área. Esto promedia el brillo del objeto en todo el objeto.
Brillo superficial (SB) cuantifica el brillo aparente o la densidad de flujo por unidad de área angular de un objeto espacialmente extendido como una galaxia o nebulosa o del fondo del cielo nocturno.
El brillo superficial de un objeto a menudo se expresa ya sea en magnitudes por segundo de arco cuadrado (mag/arcsec²) o magnitudes por minuto de arco cuadrado (mag/arcmin²). Aquí algunos objetos con la magnitud aparente y el brillo superficial más bajo (más brillante):
- Nebulosa de Orión: 4 m vs 17 mag/arcsec²
- Galaxia de Andrómeda: 3.4 m vs 11 mag/arcsec²
- Galaxia del Triángulo: 5.7 m vs 14.2 mag/arcsec²
- Galaxia de Bode: 6.9 m vs 25 mag/arcsec²
Sin embargo, el brillo superficial de un objeto rara vez se menciona, aunque es importante para las observaciones visuales.

Dato interesante: los ojos son mejores detectando luz de una fuente difusa, o extendida, (como las galaxias) que de una fuente puntual (como una estrella).
Esto significa que es más fácil ver objetos con un brillo difuso que objetos con una fuente puntual. El núcleo de la Galaxia de Andrómeda tiene ~11 mag/arcsec² pero aún es visible al ojo. El borde exterior de la galaxia puede ser visto con telescopios a 22mag/arcsec², ¡un objetivo mucho más tenue!
Magnitudes aparentes límite: guía para observadores
La magnitud límite es la magnitud aparente del objeto más tenue visible en el cielo. Aquí tienes una hoja de trucos que es útil para cualquier astrónomo aficionado. Te ayudará con tus observaciones.
- Límite a simple vista (cometas): 4
- Límite a simple vista (planetas y estrellas): 6,0
- Límite con binoculares 7×50: 9,5
- Límite con telescopio de 35 mm: 11,0
- Límite con telescopio de 60 mm: 12,0
- Límite con telescopio de 102 mm: 13,0
¡Ten en cuenta que la contaminación lumínica tiene un enorme efecto en el rango de magnitudes que puedes ver! Hemos proporcionado números para condiciones de observación cercanas a lo ideal, pero pueden ser diferentes para tu ubicación. Aprende cómo indicar cuán oscuro o brillante está tu cielo con nuestra escala práctica.

Por cierto, para averiguar la magnitud límite de tu telescopio (la magnitud más tenue que puedes ver con él bajo condiciones perfectas), puedes usar el Calculador de Magnitud Límite de Telescopio.
Conclusión
La magnitud es uno de los conceptos más importantes en la astronomía observacional porque responde a una de las preguntas más importantes: "¿Qué tan brillante es este objeto?". Para clasificar objetos por brillo, los astrónomos utilizan la escala de magnitud logarítmica, donde los objetos más brillantes tienen los valores más bajos. Al entender las magnitudes, los observadores aficionados pueden mejorar su capacidad para identificar y comparar el brillo de los objetos celestes.
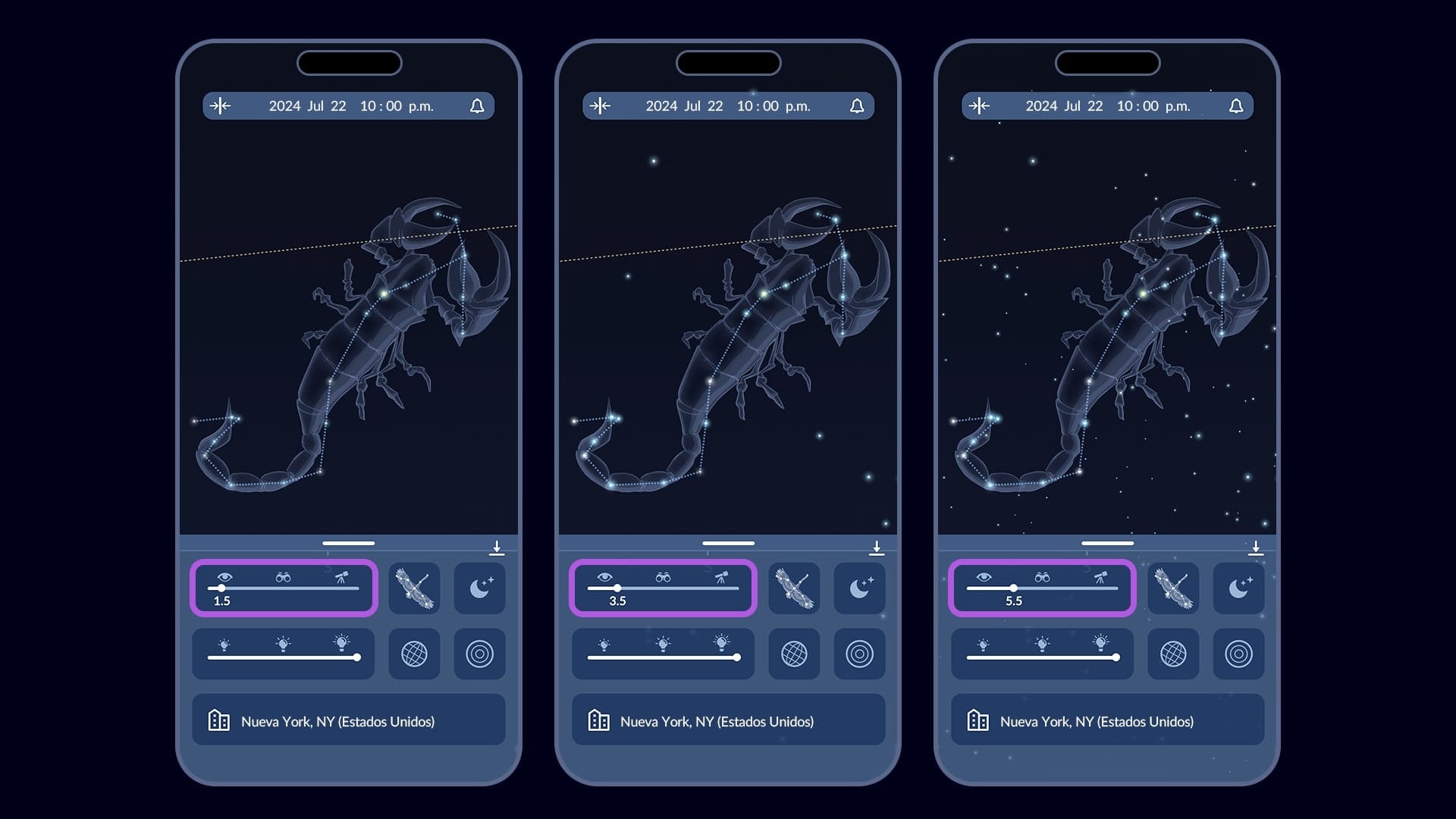
Ve los objetos más tenues en el cielo con la aplicación gratuita Sky Tonight — te permite cambiar el límite de magnitud de lo que se muestra en tu pantalla. Filtra objetos por visibilidad con un solo toque — usa iconos para el ojo desnudo, binoculares o telescopio según tu equipo.